정육면체 전개-도
백준 1917번 문제
https://www.acmicpc.net/problem/1917
1917번: 정육면체 전개도
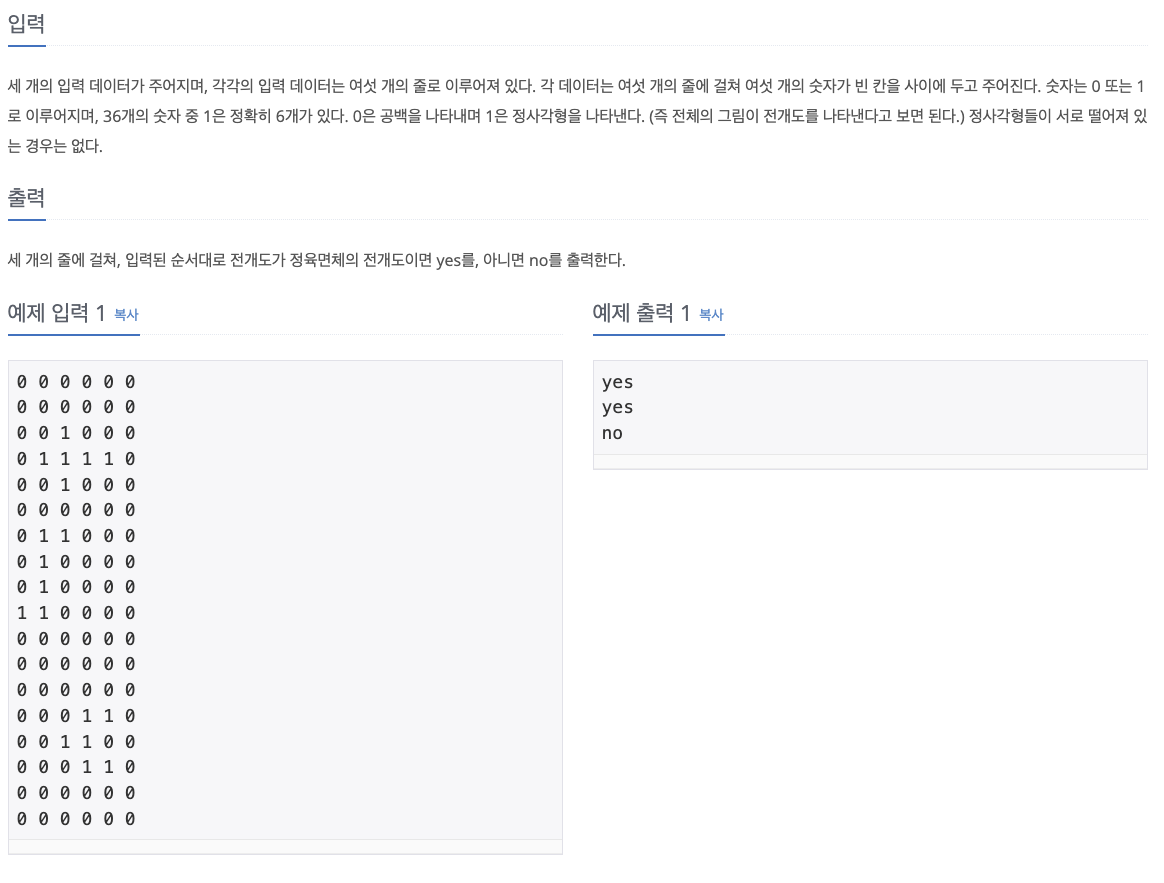
세 개의 입력 데이터가 주어지며, 각각의 입력 데이터는 여섯 개의 줄로 이루어져 있다. 각 데이터는 여섯 개의 줄에 걸쳐 여섯 개의 숫자가 빈 칸을 사이에 두고 주어진다. 숫자는 0 또는 1로 이
www.acmicpc.net
1. 문제

2. 풀이
2.1 풀이 방법
정육면체는 6개의 면으로 이루어져 있기 때문에 각 면에 번호를 붙일 수 있다.
예를 들어 정육면체가 주어졌을 때 특정 면을 0이라고 한다면 다음과 같이 번호를 붙여 볼 수 있다.
[정육면체_면 번호]

위 그림은 정육면체의 아랫면을 0이라고 했을 때, 0면을 기준으로
위 -> 1,
오른쪽 -> 2,
아래 -> 3,
왼쪽 -> 4
마주 보는 면 -> 5
로 각 면의 번호를 지정해 준 것을 나타낸다.
이 같은 방법으로 다음과 같이 예제의 첫 번째 케이스처럼 정육면체의 전개도가 주어졌을 때, 각 면에 번호를 부여할 수 있다.
[예제_1]
0 0 0 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0
0 1 1 1 1 0
0 0 1 0 0 0
0 0 0 0 0 0
[예제_1의 정육면체의 전개도_번호 부여]

여기서 각 면의 변과 연결된 면의 번호를 나타낼 수 있는데 이를 표현하면 다음과 같아진다.
[정육면체 전개도_연결된 면의 번호]

위 그림에서 0면을 보자.
0면과 위로 연결된 면은 1면, 오른쪽은 2면, 아래는 3면, 왼쪽은 4면임이 표현되어있다.
이번엔 2면을 보자
2면과 위로 연결된 면은 1면이 된다. 오른쪽은 5면, 아래는 3면, 왼쪽은 0면이다.
이처럼 각 면이 연결된 면의 번호를 나타낼수 있다면 우리는 0면부터 시작해서 주어진 전개도의 모든 면의 번호를 구할 수 있다.
[정육면체 전개도]

만약 아래와 같은 전개도가 정육면체가 되는지를 확인하려면 다음과 같은 순서를 거쳐서 확인할 수 있다.
[0 지정]
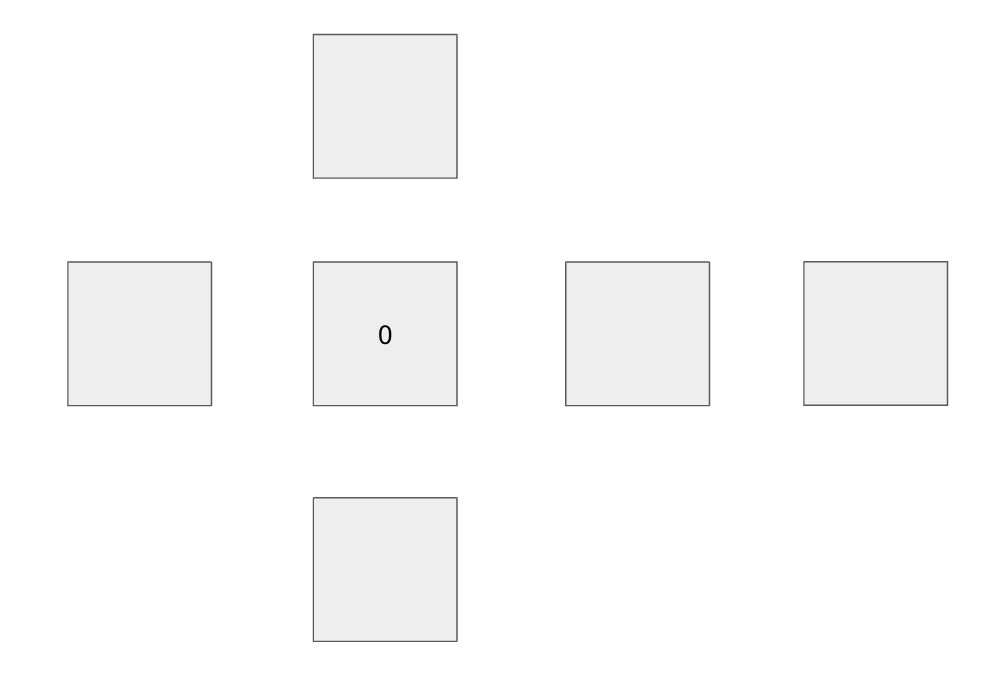
기준이 되는 0번 면을 정한다.
[0면의 변과 연결된 면의 번호 지정]
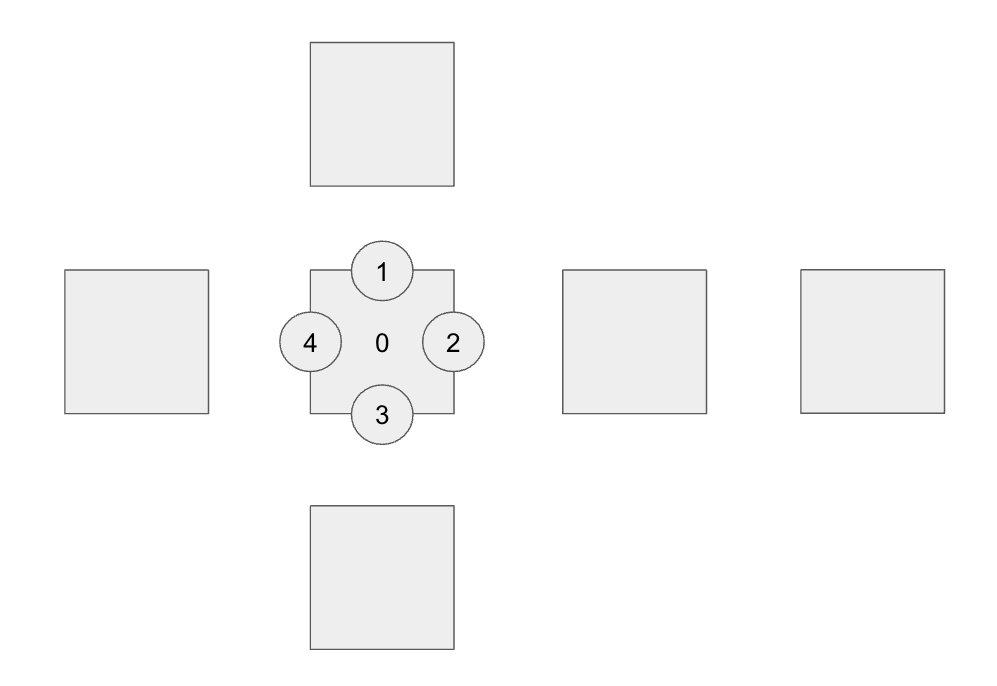
0면과 연결된 변들의 번호를 설정한다.
[전개도에서 0면과 연결된 면들의 번호를 지정한다.]

0면의 변과 연결된 면의 번호를 이용해서 0면의 변과 연결된 변들의 번호를 지정해준다.
[2면의 변과 연결된 면의 번호 설정]
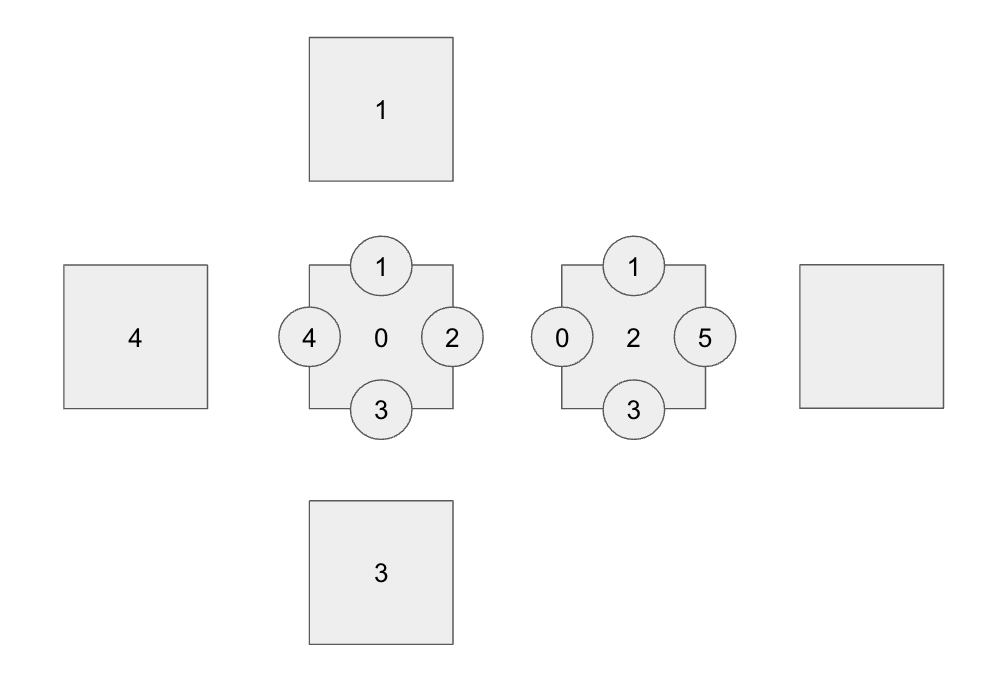
2면의 변과 연결된 면의 번호를 설정한다.
[2면과 연결된 면의 번호 지정]

2면과 연결된 면의 번호를 지정해준다.
이와 같은 식으로 특정 전개도가 주어졌을 때 0면을 정하면, 0면을 기준으로 각 면들의 번호를 지정 할 수 있다.
전개도의 모든 면의 번호를 구했을 때 겹치는 면이없다면 정육면체를 만들 수 있는 경우고 아니라면 만들 수 없는 경우이다.
0면에서부터 연결된 면을 찾을 때 0면과 연결된 면들의 번호는 바로 찾을 수 있다.
그러면 0면에서 연결된 면들에서 또 연결된 면들은 어떻게 찾을 수 있을까?
예를 들어 다음과 같이 0면에서부터 시작해서 연결된 면의 번호를 붙인다고 하자.
[0면]

전개도상 위쪽에 연결된 면이 있다고 하면 그 면은 1면이 된다.
[0과 위로 연결된 면 1면 ]

이는 0면에 표현된 0면의 변과 연결된 면의 정보를 보고 쉽게 파악할 수 있다.
전개도상 1면과 연결된 면이 있다고 한다면, 1면의 변과 연결된 면들의 번호를 구해야 한다.
그래야 1면과 연결된 면의 번호를 구할 수 있을 것이기 때문이다.
우선 각면은 특정 면과 변이 이어져있을 때 같은 연결된 면을 갖는다.
이 말이 무슨 말인지는 다음 예제를 보자.
[변이 이어지는 경우]

위 그림에서 보는 것처럼 0면에서 1면은 오른쪽 변이 이어져 있다.
전개도를 접었을 때 이 연결된 변으로 만들어지는 면이 존재할 것이다.
그 면은 0에서 오른쪽 변과 연결된 면 즉, 2면이다.
이 2면의 변은 1면의 오른쪽 변으로 이루어져 있기 때문에 당연히, 1면에서 오른쪽 변과 연결되는 면도 2면이다.
변이 연결되어있다는 것은 연결된 변으로 만들어지는 면이 동일하다는 것이다.
때문에 각면은 특정 면과 변이 이어져 있을 때 같은 연결된 면을 갖는다.
따라서 위의 성질로 다음과 같이 변이 연결된 방향의 연결된 면의 번호를 구할 수 있다.
[연결된 변을 이용]

연결된 면과 공유되는 변은 그 연결된 면의 번호를 쓰면 되기 때문에 위 그림과 같이 바로 구할 수 있다.
그렇다면 연결된 면과 반대 위치에 있는 변과 연결된 면의 번호는 어떻게 구할까?
연결된 면과 반대 위치에 있는 변과 연결된 면의 번호는 연결된 면과 마주 본 면이 된다.
이는 다음 예제를 보면 당연하다고 여겨질 수 있다.
[연결된 면과 반대 위치의 변과 연결된 면]

위 그림과 같이 0면 위에 1면과 연결되어있고 1면 위에 연결된 면이있다고 한다면..
0면을 기준으로 면하나를 두고 마주보는 면이 될 수밖에 없다.
따라서 이 경우에서 1면의 윗변과 연결되는 면은 5면이 된다.
마주 보는 면은 다음과 같다.
0 -> 5면
1 -> 3면
2-> 4면
이런 식으로, 각 변과 연결된 면들을 구할 수 있다.
2.1 코드
2.1.1 static 변수
[static 변수]
static int[] dRow = {-1, 0, 1, 0};
static int[] dCol = {0, 1, 0, -1};
static HashMap<Integer, Integer> numberSet = new HashMap<>();
static boolean result;
● dRow, dCol : 좌표를 상하좌우로 이동할 때 사용되는 배열
● numberSet : 각 면의 반대 면이 짝으로 저장되는 map
● result : 정육면체를 만들 수 있는지 없는지를 판단하는 flag
2.1.2 Plane
면을 나타내는 클래스
각 변에서 연결되는 면들의 번호를 필드로 갖고 있다.
[Plane]
//면을 나타내는 클래스
public static class Plane{
//면의 위치 번호
int number;
int row;
int col;
//면과 이어진 면들의 위치 번호를 나타내는 필드
int up;
int right;
int down;
int left;
public Plane(int number, int row, int col, int up, int right, int down, int left) {
this.number = number;
this.row = row;
this.col = col;
this.up = up;
this.right = right;
this.down = down;
this.left = left;
}
public Plane() {
}
}
2.1.3 dfs
주어진 전개도를 dfs로 탐색하며 각 면에 대응되는 Plane을 생성하고 다음 재귀 문으로 넘겨준다.
각 면을 탐색할 때 해당 면의 번호를 구하고, 만약 겹치는 면이 존재한다면 result를 false로 만들어준다.
각 면이 겹치는지는 boolean[] check 배열을 통해 확인한다.
[dfs]
public static void dfs(int[][] board, boolean[] check, Plane plane) {
for (int i = 0; i < 4; i++) {
int nextRow = plane.row + dRow[i];
int nextCol = plane.col + dCol[i];
if (nextRow < 0 || nextRow >= board.length || nextCol < 0 || nextCol >= board[0].length
|| board[nextRow][nextCol] != 1) {
continue;
}
Plane nextPlane = new Plane();
//연결된 면의 변이 이어져있으면 해당 변과 연결된 위치 번호가 이어진다.
if (dRow[i] != 0) {
if (dRow[i] == 1) {
nextPlane = new Plane(plane.down, nextRow, nextCol, plane.number,
plane.right, numberSet.get(plane.number), plane.left);
} else {
nextPlane = new Plane(plane.up, nextRow, nextCol, numberSet.get(plane.number),
plane.right, plane.number, plane.left);
}
} else {
if (dCol[i] == 1) {
nextPlane = new Plane(plane.right, nextRow, nextCol, plane.up,
numberSet.get(plane.number), plane.down, plane.number);
} else {
nextPlane = new Plane(plane.left, nextRow, nextCol, plane.up,
plane.number, plane.down, numberSet.get(plane.number));
}
}
//정육면체의 위치번호가 겹치면 정육면체를 만들 수 없다.
if (check[nextPlane.number]) {
result = false;
return;
}
check[nextPlane.number] = true;
//board에서 탐색한 위치는 0으로 만들어서 다시 탐색하지 않도록 한다.
board[plane.row][plane.col] = 0;
dfs(board, check, nextPlane);
}
}
2.1.4 main
각 케이스에 대한 초기화와 dfs메서드를 사용해 정육면체를 만들 수 있는지 여부를 판단해 "yes" 또는 "no"를 출력한다.
[main]
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//면의 반대 위치 설정
numberSet.put(0, 5);
numberSet.put(5, 0);
numberSet.put(1, 3);
numberSet.put(3, 1);
numberSet.put(2, 4);
numberSet.put(4, 2);
for (int k = 0; k < 3; k++) {
//초기화 시작
int[][] board = new int[6][6];
boolean[] check = new boolean[6];
Plane firstPlane = new Plane();
result = true;
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
int element = scanner.nextInt();
//탐색을 시작할 첫번재 plane 설정
if (!check[0] && element == 1) {
firstPlane = new Plane(0, i, j, 1, 2, 3, 4);
check[0] = true;
}
board[i][j] = element;
}
}
//초기화 끝
dfs(board, check, firstPlane);
if (result) {
System.out.println("yes");
} else {
System.out.println("no");
}
}
}
'알고리즘 > Implementation' 카테고리의 다른 글
| 미세먼지 안-녕! (0) | 2022.07.08 |
|---|---|
| A-C (0) | 2022.05.15 |

댓글