부분수-열의 합 그 2
백준 1208번 문제
https://www.acmicpc.net/problem/1208
1208번: 부분수열의 합 2
첫째 줄에 정수의 개수를 나타내는 N과 정수 S가 주어진다. (1 ≤ N ≤ 40, |S| ≤ 1,000,000) 둘째 줄에 N개의 정수가 빈 칸을 사이에 두고 주어진다. 주어지는 정수의 절댓값은 100,000을 넘지 않는다.
www.acmicpc.net
1. 문제

2. 풀이
2.1 풀이 방법
주어진 수열의 부분 수열의 합을 조합을 이용해서 구하고 그 값이 S일 때 count를 하는 방식으로 해당 문제의 답을 구할 수 있다.
그러나 이 문제에서 수열의 길이 N의 최댓값은 40이다.
즉, 부분 수열을 구하는 경우가 최대 2^40 이 될 수 있다.
따라서 단순히 주어진 수열의 부분 수열의 합을 하나씩 다 구해서 S와 비교하는 방법은 시간 초과가 발생한다.
대신 다음과 같은 방법으로 문제를 해결 할 수 있다.
1. 주어진 수열을 반으로 나누어서 각 수열의 부분 수열의 합을 구한다.
[수열 반갈]

반으로 나누어진 수열의 부분수열 합을 구하는 경우는 각각 최대 2^20 이므로 2^40에 비해 시간 제약이 훨씬 여유롭다.
[각 수열의 부분 수열의 합]

위 그림과 같이 각 수열의 부분수열의 합을 구해서 배열로 저장한다.
2. twoPointer를 사용해 두 배열에서 하나씩 선택한 원소의 합이 target값과 일치하는 모든 경우를 찾는다.
[twoPointer 적용]

start는 한쪽 배열의 시작점, end는 다른 한 쪽 배열의 끝으로 설정한다.
※ twoPointer를 적용하기 위해서는 각 배열이 정렬된 상태가 돼야 되기 때문에 배열을 정렬해준다.
각 포인터의 원소의 합이 target보다 작다면 start를 오른쪽으로,
target보다 크다면 end를 왼쪽으로 옮기며 target 값과 일치하는 경우를 찾는다.
※ 이와 같은 twoPointer 방식을 사용하면 각 포인터의 원소 합이 target이 되는 모든 경우를 탐색할 수 있다.
[twoPointer 적용2]

위 그림과 같이 포인터가 가리키는 원소의 합이 target이 된다면 count를 한다.
단, 각 포인터가 가르키는 원소가 연속되는 개수를 구해서 곱한 값을 count에 더해준다.
[count]

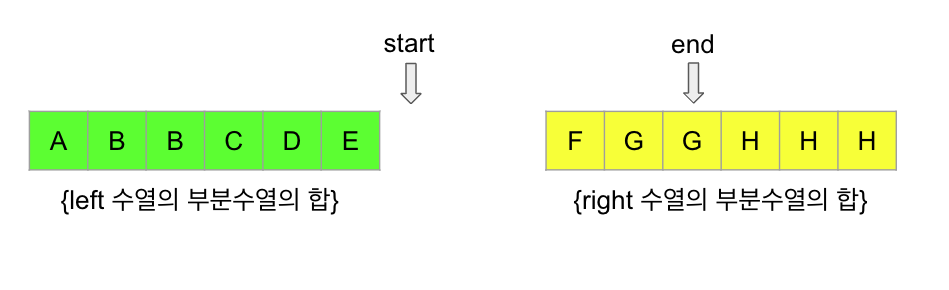
예를 들어 위 그림과 같이 start가 가르키는 B가 2개 존재하고, end가 가르키는 H가 3개 존재한다면 각 원소들로 만들 수 있는 경우는 다음과 같다.
left수열[1] + right수열[3]
left수열[1] + right수열[4]
left수열[1] + right수열[5]
left수열[2] + right수열[3]
left수열[2] + right수열[4]
left수열[2] + right수열[5]
각 배열의 원소는 합의 값이 같은 것이지 서로 다른 부분 수열의 합이기 때문에 위와 같이 경우의 수를 계산한다.
위 과정을 반복하고 포인터가 각 배열의 범위를 벗어나면 반복을 종료한다.
[twoPointer 적용 3]
3. 각 배열의 원소가 target이 되는 경우를 count 한다.
앞서 경우는 두 배열에서 하나씩 선택한 값의 합이 target과 일치하는 경우를 count 했다.
그러나 한쪽 배열을 선택하지 않는 경우도 있다.
즉, 다른 한쪽 배열의 원소 하나만으로 target과 일치하는 경우도 존재하는 것이다.
이를 count 해준다.
[각 배열 원소 count]

2.2 코드
2.2.1 combination
수열(sequence)에서 max길이의 부분 수열을 구해서 combSum에 넣어주는 메서드
[combination]
//max 만큼의 수를 선택해서 더한 값을 combSum에 넣어주는 메서드
public static void combination(int[] sequence, ArrayList<Integer> combSum, int sum, int index,
int depth, int max) {
if (depth == max) {
combSum.add(sum);
return;
}
for (int i = index; i < sequence.length; i++) {
sum += sequence[i];
combination(sequence, combSum, sum, i + 1, depth + 1, max);
sum -= sequence[i];
}
}
2.2.2 getSumOfSubSequence
수열(sequence)의 부분 수열의 합을 구하고 combSum에 넣어주는 메서드
[getSumOfSubSequence]
//부분 수열의 합을 구하는 메서드
private static void getSumOfSubSequence(int size, int[] sequence, ArrayList<Integer> combSum) {
for (int i = 1; i <= size; i++) {
combination(sequence, combSum, 0, 0, 0, i);
}
}
2.2.3 countTarget
두 리스트에서 선택한 원소가 target이 되는 경우를 count 하는 메서드
result는 static 변수로 초기화돼있다.
[countTarget]
static long result = 0;
//두개의 배열에서 뽑은 원소가 target이 되는 경우를 count하는 메서드
public static void countTarget(ArrayList<Integer> leftSumList, ArrayList<Integer> rightSumList, int target) {
//두 배열에서 원소를 뽑지않고 한쪽 배열에서만 원소를 뽑았을 때 target과 일치하는 값이 있으면 count한다.
result += Collections.frequency(rightSumList, target);
result += Collections.frequency(leftSumList, target);
//twoPointer를 사용하기 위해 정렬
leftSumList.sort(Comparator.naturalOrder());
rightSumList.sort(Comparator.naturalOrder());
int start = 0;
int end = rightSumList.size() - 1;
//시작은 leftSum의 0번 원소, 끝은 rightSum의 마지막 원소로 두고 twoPointer를 사용해 두 포인터의 합이 target이 되는 값을 찾는다.
while (start < leftSumList.size() && end >= 0) {
int sum = leftSumList.get(start) + rightSumList.get(end);
//만약 두 포인터의 합이 target과 같다면 합이 target과 같아지는 각 배열의 원소의 개수를 구해서 곱해준다.(정렬되있어서 가능)
if (sum == target) {
int leftSum = leftSumList.get(start);
int rightSum = rightSumList.get(end);
long lCount = 0;
long rCount = 0;
//현재 포인터(sum == target이 되는 위치)로부터 leftSumList 또는 rightSumList의 원소가 동일한 개수를 구한다.
while (start < leftSumList.size() && leftSumList.get(start) == leftSum) {
start++;
lCount++;
}
while (end >= 0 && rightSumList.get(end) == rightSum) {
end--;
rCount++;
}
result += lCount * rCount;
}
if (sum < target) {
start++;
} else if (sum > target){
end--;
}
}
}
각 리스트의 원소만으로 target이 되는 경우를 먼저 count를 해주었다.
2.2.4 main
[main]
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int size = scanner.nextInt();
int target = scanner.nextInt();
int[] sequence = new int[size];
for (int i = 0; i < size; i++) {
sequence[i] = scanner.nextInt();
}
int middle = (size - 1) / 2;
int[] leftSequence = Arrays.copyOfRange(sequence, 0, middle);
int[] rightSequence = Arrays.copyOfRange(sequence, middle, size);
ArrayList<Integer> leftSumList = new ArrayList<>();
ArrayList<Integer> rightSumList = new ArrayList<>();
getSumOfSubSequence(size, leftSequence, leftSumList);
getSumOfSubSequence(size, rightSequence, rightSumList);
countTarget(leftSumList, rightSumList, target);
System.out.println(result);
}
3. 전체 코드
[전체 코드]
import java.util.*;
public class 부분수열의합2_1208 {
static long result = 0;
//max 만큼의 수를 선택해서 더한 값을 combSum에 넣어주는 메서드
public static void combination(int[] sequence, ArrayList<Integer> combSum, int sum, int index,
int depth, int max) {
if (depth == max) {
combSum.add(sum);
return;
}
for (int i = index; i < sequence.length; i++) {
sum += sequence[i];
combination(sequence, combSum, sum, i + 1, depth + 1, max);
sum -= sequence[i];
}
}
//부분 수열의 합을 구하는 메서드
private static void getSumOfSubSequence(int size, int[] sequence, ArrayList<Integer> combSum) {
for (int i = 1; i <= size; i++) {
combination(sequence, combSum, 0, 0, 0, i);
}
}
//두개의 배열에서 뽑은 원소가 target이 되는 경우를 count하는 메서드
public static void countTarget(ArrayList<Integer> leftSumList, ArrayList<Integer> rightSumList, int target) {
//두 배열에서 원소를 뽑지않고 한쪽 배열에서만 원소를 뽑았을 때 target과 일치하는 값이 있으면 count한다.
result += Collections.frequency(rightSumList, target);
result += Collections.frequency(leftSumList, target);
//twoPointer를 사용하기 위해 정렬
leftSumList.sort(Comparator.naturalOrder());
rightSumList.sort(Comparator.naturalOrder());
int start = 0;
int end = rightSumList.size() - 1;
//시작은 leftSum의 0번 원소, 끝은 rightSum의 마지막 원소로 두고 twoPointer를 사용해 두 포인터의 합이 target이 되는 값을 찾는다.
while (start < leftSumList.size() && end >= 0) {
int sum = leftSumList.get(start) + rightSumList.get(end);
//만약 두 포인터의 합이 target과 같다면 합이 target과 같아지는 각 배열의 원소의 개수를 구해서 곱해준다.(정렬되있어서 가능)
if (sum == target) {
int leftSum = leftSumList.get(start);
int rightSum = rightSumList.get(end);
long lCount = 0;
long rCount = 0;
//현재 포인터(sum == target이 되는 위치)로부터 leftSumList 또는 rightSumList의 원소가 동일한 개수를 구한다.
while (start < leftSumList.size() && leftSumList.get(start) == leftSum) {
start++;
lCount++;
}
while (end >= 0 && rightSumList.get(end) == rightSum) {
end--;
rCount++;
}
result += lCount * rCount;
}
if (sum < target) {
start++;
} else if (sum > target){
end--;
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int size = scanner.nextInt();
int target = scanner.nextInt();
int[] sequence = new int[size];
for (int i = 0; i < size; i++) {
sequence[i] = scanner.nextInt();
}
int middle = (size - 1) / 2;
int[] leftSequence = Arrays.copyOfRange(sequence, 0, middle);
int[] rightSequence = Arrays.copyOfRange(sequence, middle, size);
ArrayList<Integer> leftSumList = new ArrayList<>();
ArrayList<Integer> rightSumList = new ArrayList<>();
getSumOfSubSequence(size, leftSequence, leftSumList);
getSumOfSubSequence(size, rightSequence, rightSumList);
countTarget(leftSumList, rightSumList, target);
System.out.println(result);
}
}
댓글