내리막-길
백준 1520번 문제
https://www.acmicpc.net/problem/1520
1520번: 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
1. 문제


2. 풀이
2.1 풀이 방법
d(i, j) 를 시작점에서부터 i, j로 갈 수 있는 경우의 수를 의미한다고 하자.
그러면 다음과 같은 점화식이 성립한다.
d(i, j) = SUM(d(i - 1, j), d(i, j + 1), d(i + 1, j), d(i, j - 1)) (단, (i,j)의 높이보다 높을 경우만 더해준다.)
따라서 도착점을 (i, j)라고 할 때, 도착점에서부터 해당 점화식으로 d(i, j)의 값을 구하면 된다(TopDown 방식).
중요한 것은 점화식을 사용해서 특정 d()를 구할 때, d(i - 1, j), d(i, j + 1), d(i + 1, j), d(i, j - 1) 중, 이미 구해진 값이 있다면 추가적으로 점화식을 사용하지 않고 구해진 값을 쓰는 것이다.
문제의 첫 번째 예시에서 주어진 4x5의 배열에서의 답을 위의 점화식을 사용해서 구한다고 하자.
[dp 예_그 1]

도착점, d(4, 5)의 값을 구해야 한다.
점화식에 따르면 d(4, 5) = SUM(d(4, 4), d(3, 5)) 이다.
[d(4, 5)]

d(4, 4)(15)와 d(3, 5)(28)의 값은 아직 구해지지 않았기 때문에 다시 점화식을 통해 그 값을 구해주어야 한다.
여기서는 우선 d(4, 4)(15)의 값을 구해보자.
d(4, 4) = SUM(d(4, 3), d(3, 4)) 이다.
[d(4, 4)]

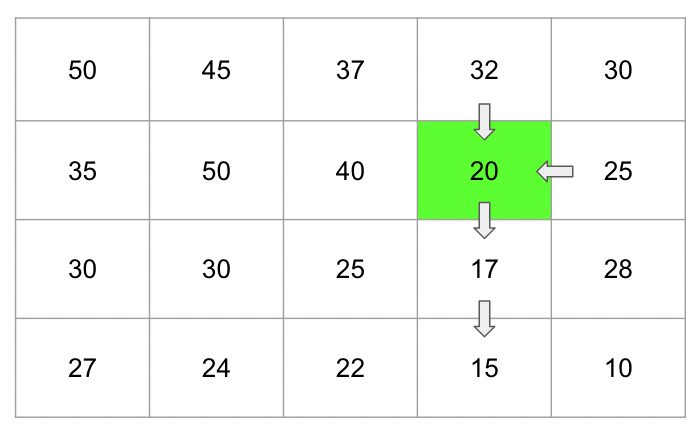
위와 같이 점화식을 사용해서 재귀적으로 값을 구하다 보면 d(2, 4)(20)을 구해야 한다.
d(2, 4) = SUM(d(1, 4), d(2, 5), d(2, 3)) 이다.
d(2, 3)(40)의 경우 출발점에 도착할 수 없기 때문에 d(2, 3) = 0이 된다.
따라서 우선 d(1, 4)(32)와 d(2, 5)(25)의 경우를 보자.
[d(2, 4)]
d(1, 4)(32)의 값을 점화식을 사용해서 구하면 다음과 같은 경로로 출발점에 도달한다.
출발점에서 출발점으로 가는 경우의 수는 1(d(1,1) = 1)이므로 아래와 같이 1의 값이 재귀적으로 더해진다.
결과적으로 출발 지점에서부터 (1, 4)으로 가는 경우는 1이므로 d(1, 4) = 1이 된다.
[d(1, 4)]

이번에는 d(2, 5)(25)를 구해야 한다.
d(2, 5) = SUM(d(1, 5)) 이다.
[d(2, 5)]

d(1, 5)(30)의 값은 다음과 같이 구할 수 있다.
d(1, 5) = SUM(d(1, 4))
[d(1, 5)]

그런데 앞에서 d(1, 4)(32)의 값은 1로 이미 구해졌었다.
따라서 재귀적으로 값을 탐색하지 않고 구해진 d(1, 4)의 값을 바로 사용하면 된다.
d(1, 5) = SUM(d(1, 4)) 이므로
d(1, 5) = 1 이 된다.
따라서 다음과 같이 d(2, 4)를 구할 수 있다.
d(2, 4) = SUM(d(1, 4), d(2, 5), d(2, 3)) = SUM(1, 1, 0) = 2
[d(2, 4)의 값 계산]

이와 같은 방식으로 점화식을 사용해 재귀적으로 d(i, j)의 값을 구할 수 있으며, 중복된 연산을 피할 수 있다.
2.2 코드
2.2.1 Node & static
[Node & static]
static int[] dRow = {-1, 0, 1, 0};
static int[] dCol = {0, 1, 0, -1};
private static class Node {
private int row;
private int col;
private int height;
//시작점에서 해당 노드로 갈 수 있는 경우의 수
private int caseNumber = 0;
private boolean check = false;
public Node(int row, int col, int height) {
this.row = row;
this.col = col;
this.height = height;
}
}
check는 해당 노드 위치의 d(row, col)이 계산된 경우 true가 된다.
2.2.2 dp
점화식을 사용해서 주어진 노드 위치의 d(row, col)을 구한다.
[dp]
//점화식 : d[i][j]를 시작점에서 해당 위치로 갈 수 있는 경우의 수라고 한다면
//d[i][j] = sum(d[i - 1][j], d[i][j + 1], d[i - 1][j], d[i][j - 1])
private static Node dp(Node node, Node[][] nodeArr, Node startNode) {
//해당 노드의 caseNumber가 계산됬다면 점화식을 돌리지 않고 바로 그 노드를 반환
if (node.check) {
return node;
}
if (node == startNode) {
return startNode;
}
//d[i][j] = sum(d[i - 1][j], d[i][j + 1], d[i - 1][j], d[i][j - 1])
//d[i][j] = nodeArr[i][j].caseNumber
//nodeArr[i - 1][j], nodeArr[i][j + 1], nodeArr[i - 1][j], nodeArr[i][j - 1] 에서
//nodeArr[i][j]보다 높이가 낮은 node는 제외
for (int i = 0; i < 4; i++) {
int beforeRow = node.row + dRow[i];
int beforeCol = node.col + dCol[i];
if (beforeRow < 0 || beforeRow >= nodeArr.length || beforeCol < 0 || beforeCol >= nodeArr[0].length
|| nodeArr[beforeRow][beforeCol].height <= node.height) {
continue;
}
Node beforeNode = dp(nodeArr[beforeRow][beforeCol], nodeArr, startNode);
node.caseNumber += beforeNode.caseNumber;
}
node.check = true;
return node;
}
2.2.3 main
[main]
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int rowSize = Integer.parseInt(st.nextToken());
int colSize = Integer.parseInt(st.nextToken());
Node[][] nodeArr = new Node[rowSize][colSize];
for (int i = 0; i < rowSize; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < colSize; j++) {
nodeArr[i][j] = new Node(i, j, Integer.parseInt(st.nextToken()));
}
}
nodeArr[0][0].caseNumber = 1;
dp(nodeArr[rowSize - 1][colSize - 1], nodeArr, nodeArr[0][0]);
System.out.println(nodeArr[rowSize - 1][colSize - 1].caseNumber);
}
출발지에서 출발지로 가는 경우는 1이기 때문에, 출발지 Node의 caseNumber를 1로 세팅해준다.
3. 전체 코드
[전체 코드]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class 내리막길_1520 {
static int[] dRow = {-1, 0, 1, 0};
static int[] dCol = {0, 1, 0, -1};
private static class Node {
private int row;
private int col;
private int height;
//시작점에서 해당 노드로 갈 수 있는 경우의 수
private int caseNumber = 0;
private boolean check = false;
public Node(int row, int col, int height) {
this.row = row;
this.col = col;
this.height = height;
}
}
//점화식 : d[i][j]를 시작점에서 해당 위치로 갈 수 있는 경우의 수라고 한다면
//d[i][j] = sum(d[i - 1][j], d[i][j + 1], d[i - 1][j], d[i][j - 1])
private static Node dp(Node node, Node[][] nodeArr, Node startNode) {
//해당 노드의 caseNumber가 계산됬다면 점화식을 돌리지 않고 바로 그 노드를 반환
if (node.check) {
return node;
}
if (node == startNode) {
return startNode;
}
//d[i][j] = sum(d[i - 1][j], d[i][j + 1], d[i - 1][j], d[i][j - 1])
//d[i][j] = nodeArr[i][j].caseNumber
//nodeArr[i - 1][j], nodeArr[i][j + 1], nodeArr[i - 1][j], nodeArr[i][j - 1] 에서
//nodeArr[i][j]보다 높이가 낮은 node는 제외
for (int i = 0; i < 4; i++) {
int beforeRow = node.row + dRow[i];
int beforeCol = node.col + dCol[i];
if (beforeRow < 0 || beforeRow >= nodeArr.length || beforeCol < 0 || beforeCol >= nodeArr[0].length
|| nodeArr[beforeRow][beforeCol].height <= node.height) {
continue;
}
Node beforeNode = dp(nodeArr[beforeRow][beforeCol], nodeArr, startNode);
node.caseNumber += beforeNode.caseNumber;
}
node.check = true;
return node;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int rowSize = Integer.parseInt(st.nextToken());
int colSize = Integer.parseInt(st.nextToken());
Node[][] nodeArr = new Node[rowSize][colSize];
for (int i = 0; i < rowSize; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < colSize; j++) {
nodeArr[i][j] = new Node(i, j, Integer.parseInt(st.nextToken()));
}
}
nodeArr[0][0].caseNumber = 1;
dp(nodeArr[rowSize - 1][colSize - 1], nodeArr, nodeArr[0][0]);
System.out.println(nodeArr[rowSize - 1][colSize - 1].caseNumber);
}
}
'알고리즘 > DP' 카테고리의 다른 글
| LCS (1) | 2023.06.04 |
|---|---|
| 가장 긴 증가하는 부분 수열 (0) | 2023.01.16 |
| Word Break (0) | 2022.06.19 |
| Longest Increasing Path in a Matrix (0) | 2022.06.13 |
| 합-분해 (0) | 2022.04.29 |



댓글