줄-세우기
백준 2252번 문제
https://www.acmicpc.net/problem/2252
2252번: 줄 세우기
첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의
www.acmicpc.net
1. 문제
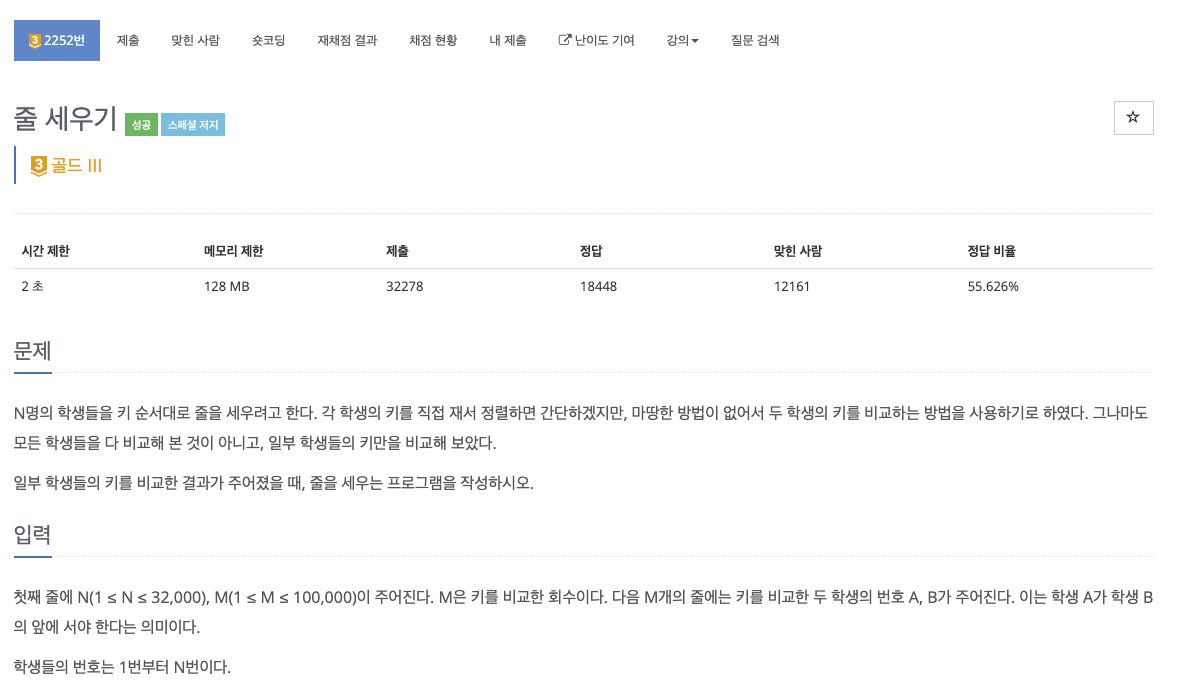
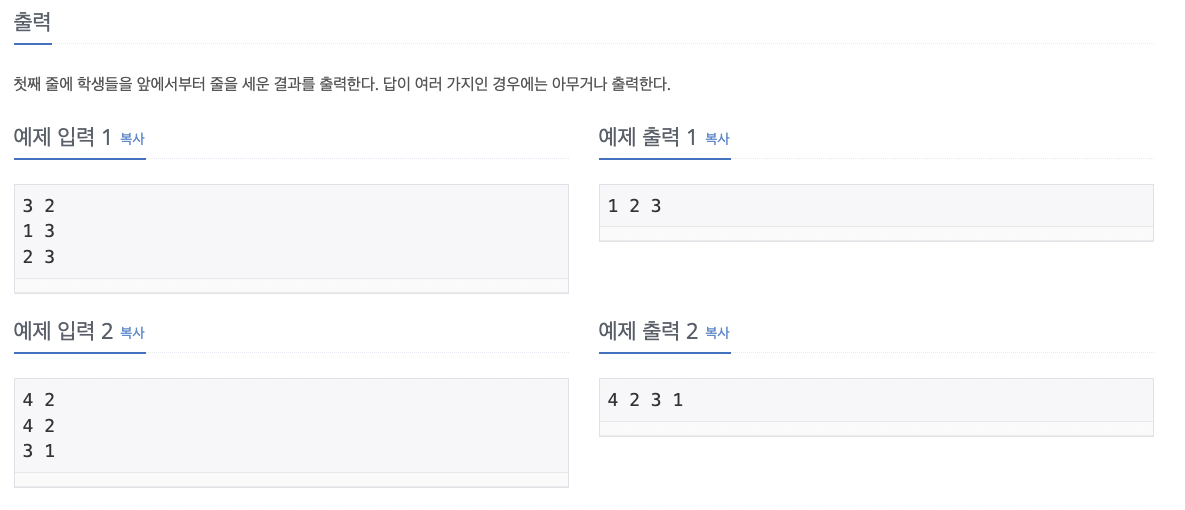
2. 풀이
2.1 풀이 방법
이 문제에서 학생들의 키를 비교한 관계를 그래프로 나타내면 DAG(Directed Acyclic Graph)가 된다.
따라서 학생들의 키를 위상 정렬을 사용해서 정렬할 수 있다.
2.1.2 Directed Acyclic Graph
DAG는 말 그대로 사이클이 없는 방향 있는 그래프를 의미한다.
예를 들어 문제의 입력이 다음과 같이 들어온다고 하자
[입력 예]
5 5
2 1
3 2
3 5
4 2
5 1
학생 A의 키가 학생 B보다 작은 것을 A -> B로 표현한다면,
그래프를 다음과 같이 구성 할 수 있다.
[DAG 예]
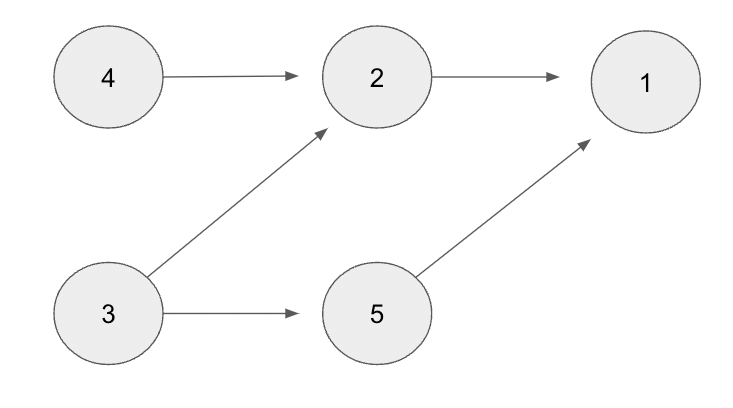
학생들의 키는 비교 결과에 따라 위와 같이 방향 있는 간선으로 관계를 나타낼 수 있으며, A가 B보다 작고 B가 C보다 작을 때, C가 A보다 작을 수는 없기 때문에 순환이 일어나지 않는다.
따라서 이 문제에서 학생들의 키는 DAG로 나타낼 수 있다.
2.1.2 위상정렬
위상 정렬은 순서가 정해져 있는 작업을 차례로 수행해야 할 때, 그 순서를 정하는 알고리즘이다.
위상 정렬은 DAG에만 적용할 수 있는 알고리즘이다.
다음과 같이 순환하는 그래프가 있다고 하자.
[순화 그래프]
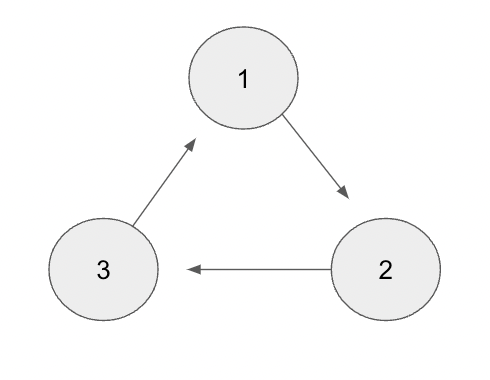
위 그래프가 작업 순서를 나타낸다고 했을 때 1을 처리 하기 위해서는 어떤 순서로 작업을 해야 할까?
1을 처리하려면 3을 처리해야 한다.
3을 처리하려면 2를 처리해야 한다.
그런데 2를 처리하려면 1을 처리해야 한다.
이 때문에 순환하는 그래프에서는 순서를 정할 수 없고 위상 정렬을 적용할 수 없다.
A학생의 키가 B학생보다 작을 때 그 관계를 A -> B로 표현한다면 앞의 예와 같이 우리는 DAG그래프를 얻을 수 있다.
따라서 이 문제에는 위상정렬을 적용해서 각 학생들의 키의 순서를 구할 수 있다.
위상 정렬은 다음과 같은 과정을 통해서 순서를 구할 수 있다.
1. 진입 차수가 0인 노드들을 Queue에 넣는다.
2. Queue에서 뺀 노드의 간선을 전부 제거한다.
3. 간선을 지우면서 간선과 연결된 노드를 탐색한다.
이를 반복했을 때, Queue에 들어온 순서가 해당 그래프의 노드들이 정렬된 순서가 된다.
문제에서 입력이 앞서 DAG의 예처럼 들어온다고 하자.
이때 다음과 같은 절차를 통해 위상 정렬을 적용해서 순서를 결정할 수 있다.
[위상정렬 예 그_1]
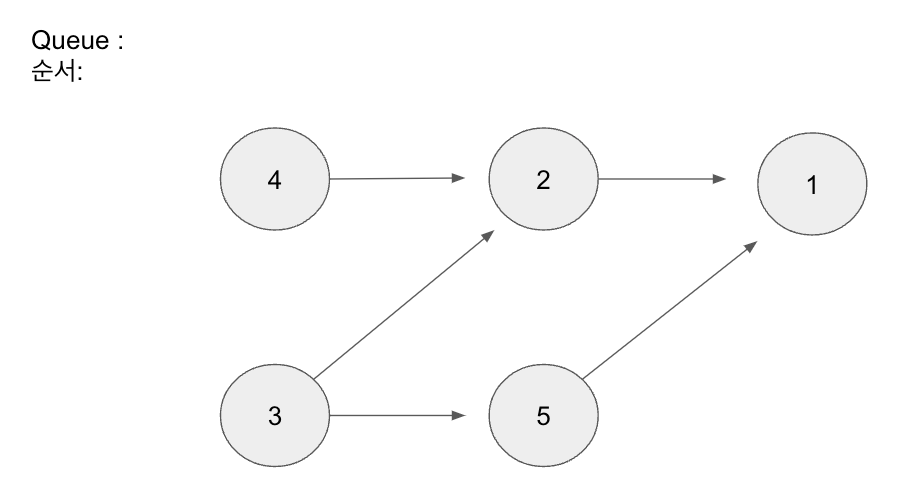
[위상정렬 예 그_2]
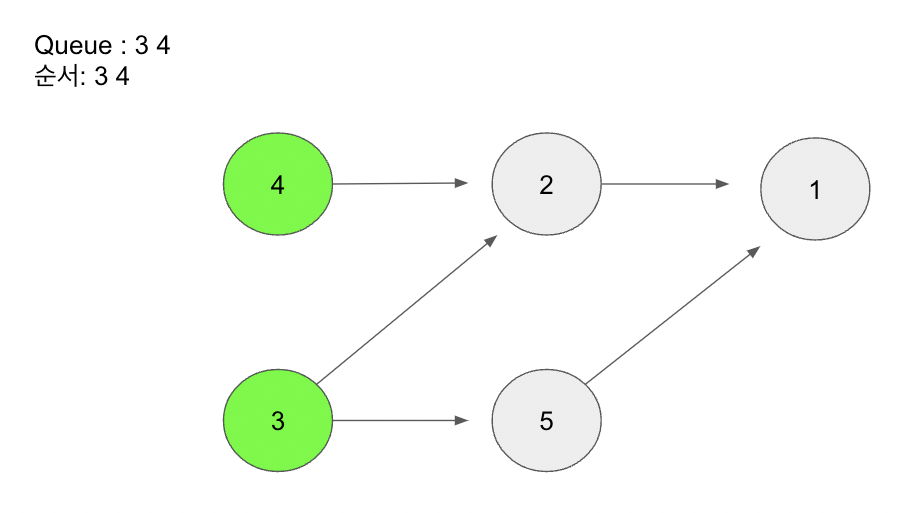
진입 차수가 0인 3과 4를 Queue에 넣어준다.
[위상정렬 예 그_3]
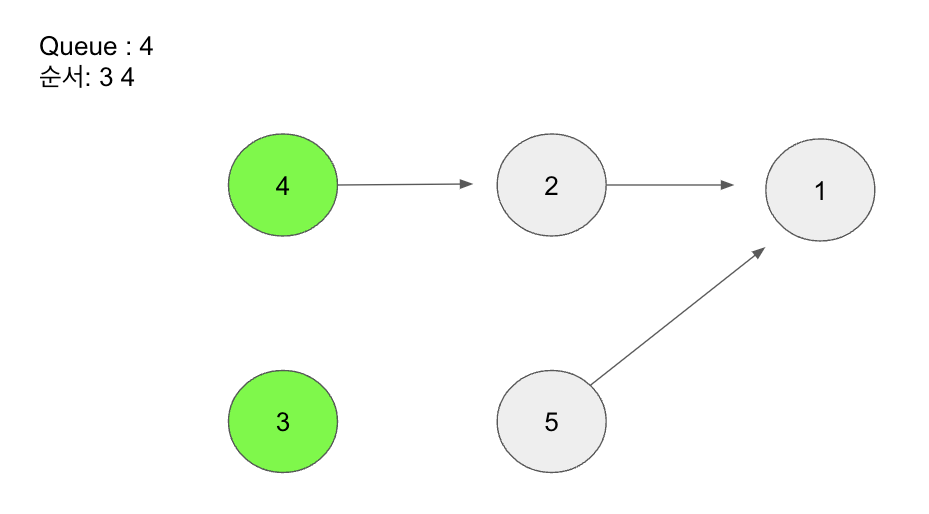
Queue에서 맨 앞에 있는 3을 빼고 3과 연결된 간선을 지워준다.
[위상정렬 예 그_4]
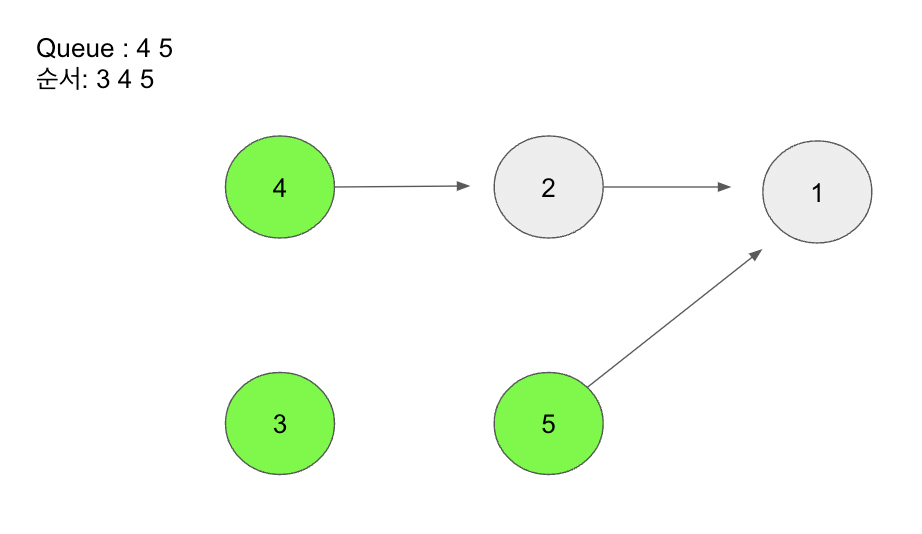
3과 간선으로 연결돼있던 5가 진입 차수가 0이 됐기 때문에 Queue에 넣어준다.
이를 다음과 같이 계속해서 반복한다.
[위상정렬 예 그_4]
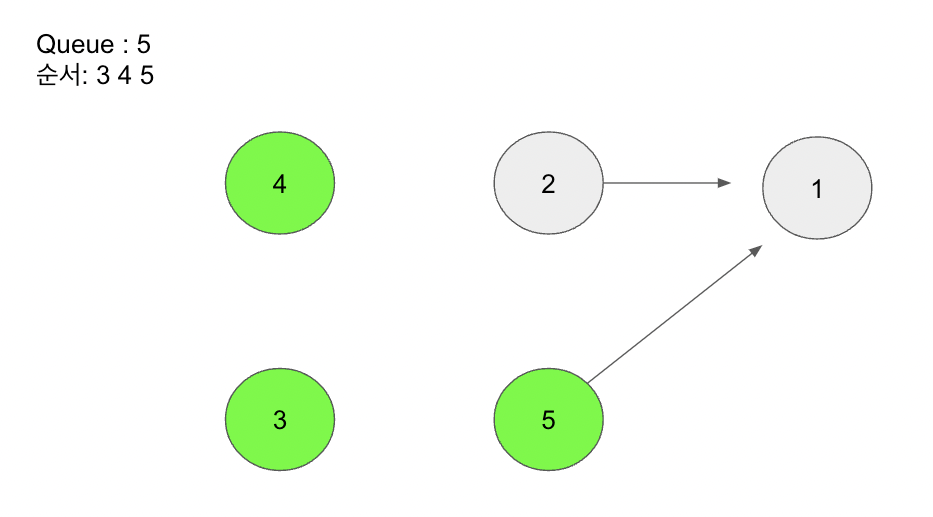
[위상정렬 예 그_5]
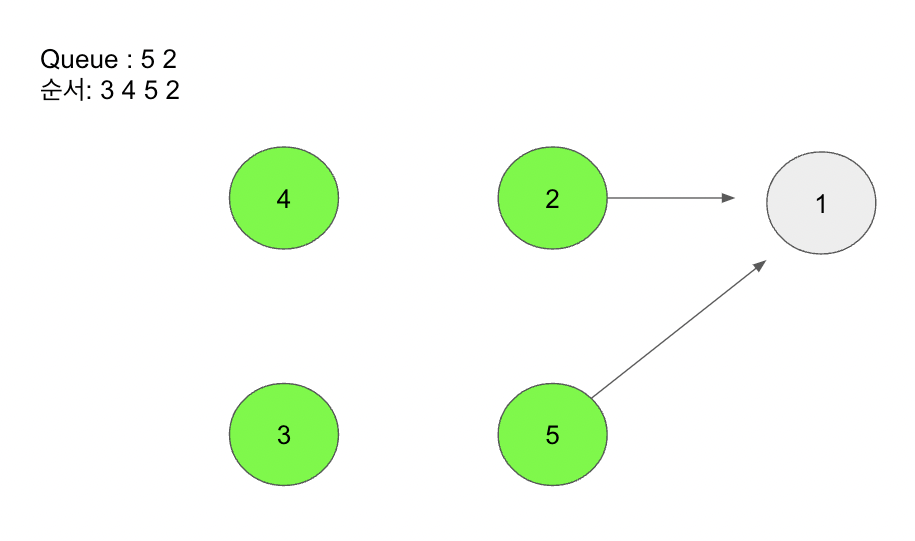
[위상정렬 예 그_6]
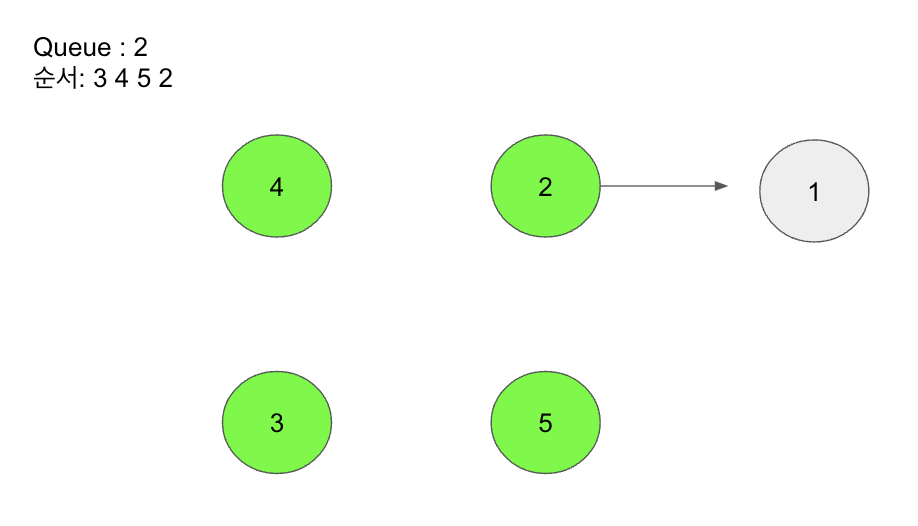
[위상정렬 예 그_7]
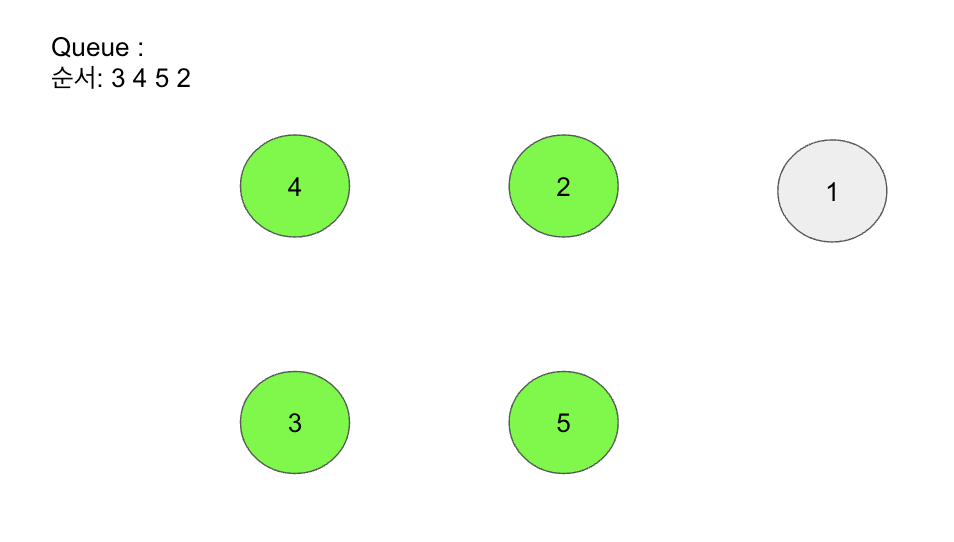
[위상정렬 예 그_8]
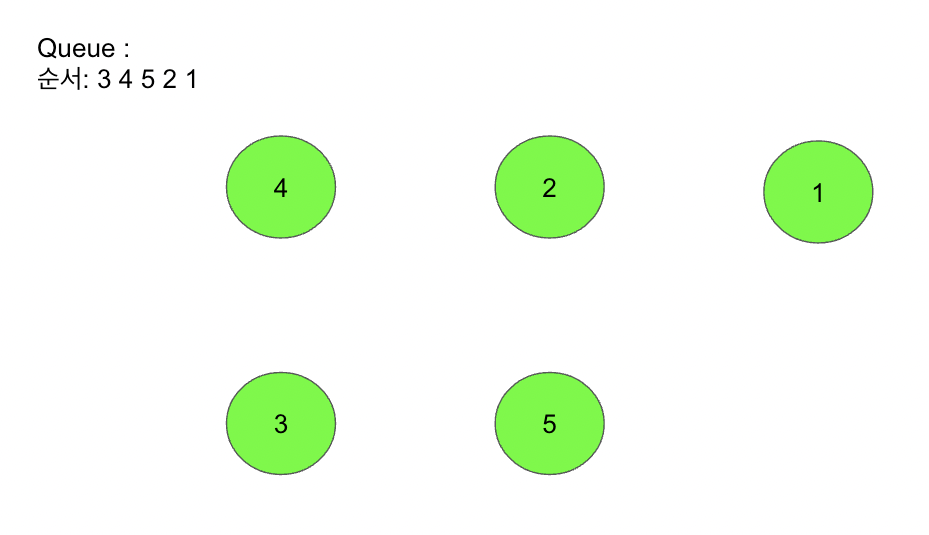
이처럼 위상 정렬을 이용해서 학생들의 키의 순서를 정할 수 있다.
2.2 코드
2.2.1 Node
노드(학생)를 나타내는 클래스
[Node]
//node를 나타내는 클래스
private static class Node {
int number;
//진입차수
int linkEdge = 0;
//간선
ArrayList<Node> edge = new ArrayList<>();
public Node(int number) {
this.number = number;
}
}
2.2.2 topologySort
위상 정렬로 주어진 그래프를 정렬하는 메서드
[topologySort]
//위상정렬된 값들을 sortResult에 넣고 반환하는 메서드
private static ArrayList<Integer> topologySort(Node[] nodeArr) {
//위상정렬된 값들이 들어갈 리스트
ArrayList<Integer> sortResult = new ArrayList<>();
Queue<Node> queue = new LinkedList<>();
//queue에 초기값으로 노드방향 간선 수가 0인 값들을 넣는다.
for (int i = 1; i < nodeArr.length; i++) {
if (nodeArr[i].linkEdge == 0) {
queue.offer(nodeArr[i]);
sortResult.add(nodeArr[i].number);
}
}
while (!queue.isEmpty()) {
Node node = queue.poll();
//반복문을 돌면서 node와 연결된 간선을 지운다.
//간선을 지운다 = 간선으로 이어진 node의 linkEdge(진입차수)에서 1을 빼줌
for (int i = 0; i < node.edge.size(); i++) {
Node linkNode = node.edge.get(i);
linkNode.linkEdge--;
if (linkNode.linkEdge == 0) {
queue.offer(linkNode);
sortResult.add(linkNode.number);
}
}
}
return sortResult;
}
2.2.3 Main
[main]
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int nodeSize = scanner.nextInt();
int edgeSize = scanner.nextInt();
Node[] nodeArr = new Node[nodeSize + 1];
for (int i = 1; i <= nodeSize; i++) {
nodeArr[i] = new Node(i);
}
for (int i = 0; i < edgeSize; i++) {
int from = scanner.nextInt();
int to = scanner.nextInt();
nodeArr[from].edge.add(nodeArr[to]);
//진입차수 증가
nodeArr[to].linkEdge++;
}
ArrayList<Integer> sortResult = topologySort(nodeArr);
sortResult.forEach(s -> System.out.print(s + " "));
}
3. 전체 코드
[전체 코드]
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class 줄세우기_2252 {
//node를 나타내는 클래스
private static class Node {
int number;
//진입차수
int linkEdge = 0;
//간선
ArrayList<Node> edge = new ArrayList<>();
public Node(int number) {
this.number = number;
}
}
//위상정렬된 값들을 sortResult에 넣고 반환하는 메서드
private static ArrayList<Integer> topologySort(Node[] nodeArr) {
//위상정렬된 값들이 들어갈 리스트
ArrayList<Integer> sortResult = new ArrayList<>();
Queue<Node> queue = new LinkedList<>();
//queue에 초기값으로 노드방향 간선 수가 0인 값들을 넣는다.
for (int i = 1; i < nodeArr.length; i++) {
if (nodeArr[i].linkEdge == 0) {
queue.offer(nodeArr[i]);
sortResult.add(nodeArr[i].number);
}
}
while (!queue.isEmpty()) {
Node node = queue.poll();
//반복문을 돌면서 node와 연결된 간선을 지운다.
//간선을 지운다 = 간선으로 이어진 node의 linkEdge(진입차수)에서 1을 빼줌
for (int i = 0; i < node.edge.size(); i++) {
Node linkNode = node.edge.get(i);
linkNode.linkEdge--;
if (linkNode.linkEdge == 0) {
queue.offer(linkNode);
sortResult.add(linkNode.number);
}
}
}
return sortResult;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int nodeSize = scanner.nextInt();
int edgeSize = scanner.nextInt();
Node[] nodeArr = new Node[nodeSize + 1];
for (int i = 1; i <= nodeSize; i++) {
nodeArr[i] = new Node(i);
}
for (int i = 0; i < edgeSize; i++) {
int from = scanner.nextInt();
int to = scanner.nextInt();
nodeArr[from].edge.add(nodeArr[to]);
//진입차수 증가
nodeArr[to].linkEdge++;
}
ArrayList<Integer> sortResult = topologySort(nodeArr);
sortResult.forEach(s -> System.out.print(s + " "));
}
}
'알고리즘 > Graph' 카테고리의 다른 글
| 키 순-서 & 플로이드-워셜 알고리즘 (0) | 2024.08.02 |
|---|---|
| LCA2 (0) | 2023.02.20 |
| Union-Find 알고리즘을 케이크처럼 쉽게 이해하는법 (0) | 2023.02.07 |



댓글