LCA2
백준 11438번 문제
https://www.acmicpc.net/problem/11438
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
1. 문제
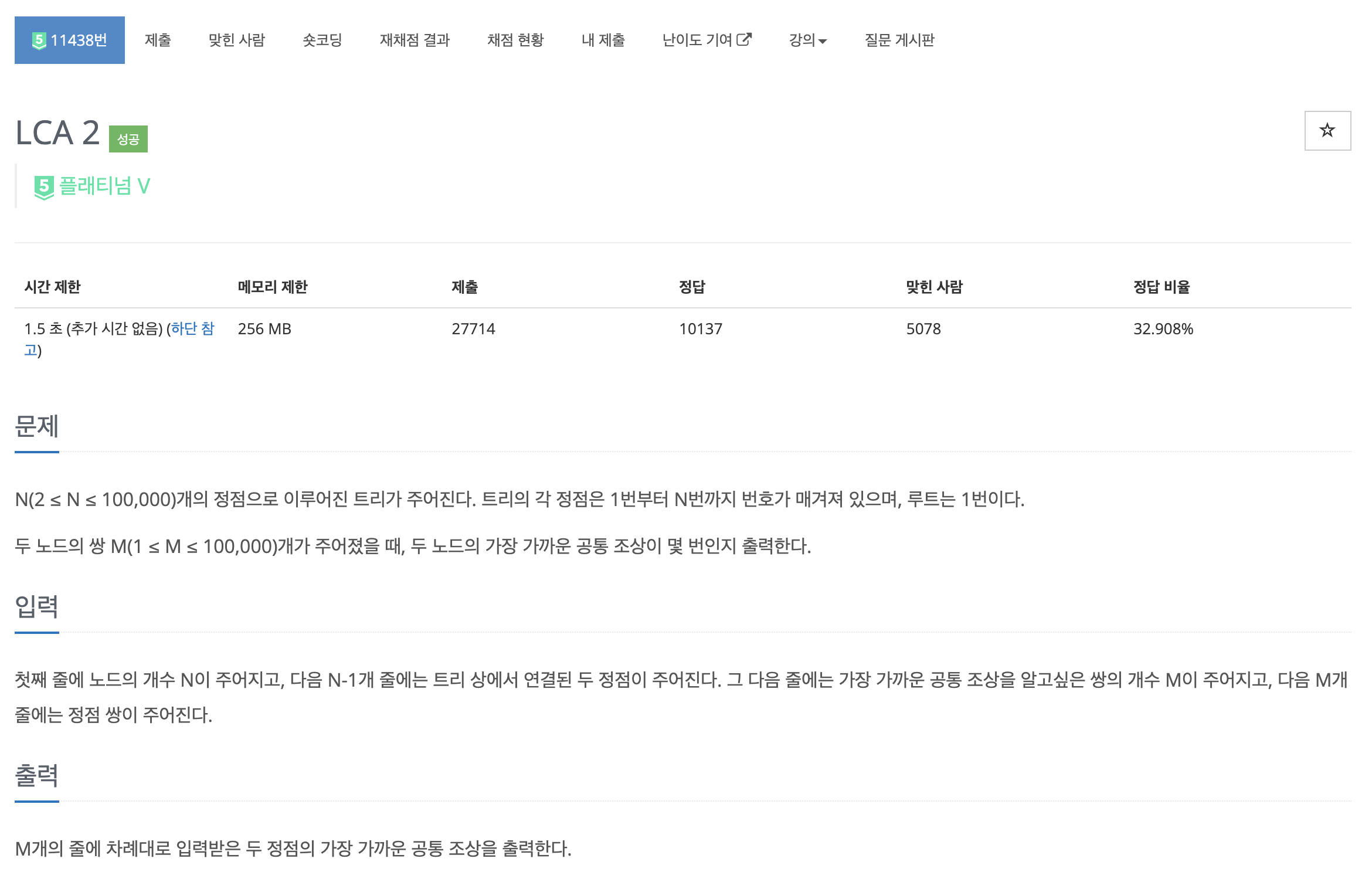
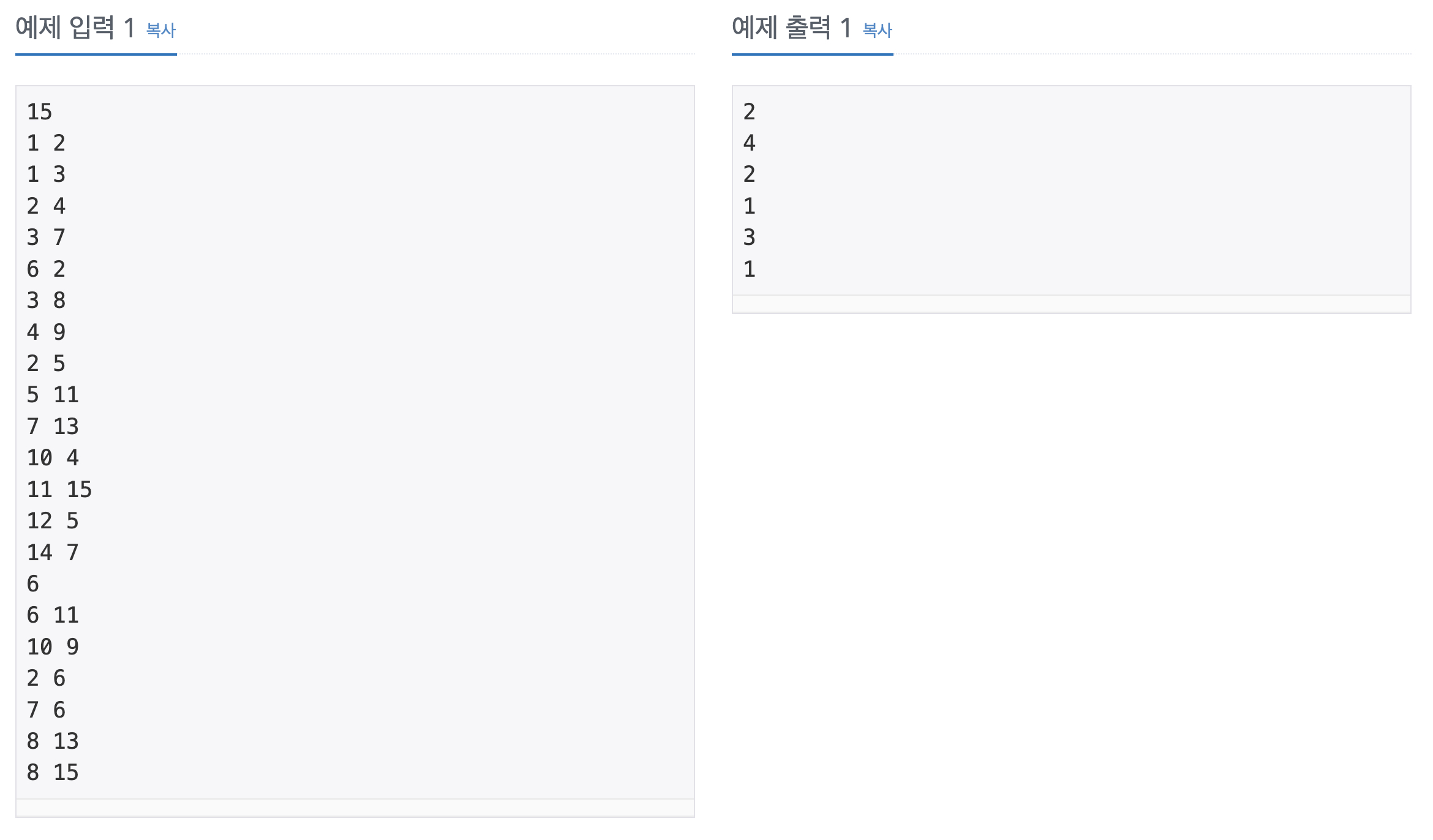
2. 풀이
2.1 풀이 방법
2.1.1 LCA
트리에서 공통의 조상을 찾는 것은 LCA 알고리즘을 통해 해결할 수 있다.
LCA 알고리즘은 다음과 같은 과정으로 두 노드 간의 공통 조상을 찾는다.
1. 두 노드의 깊이가 다르면 같아질 때까지 한쪽 노드의 깊이를 올린다.
2. 두 노드가 같아질때까지 깊이를 한칸씩 올린다.
다음과 같은 트리가 주어졌을 때 4번 노드와 8번 노드의 공통 조상을 찾는다고 하자.
[LCA 예시]
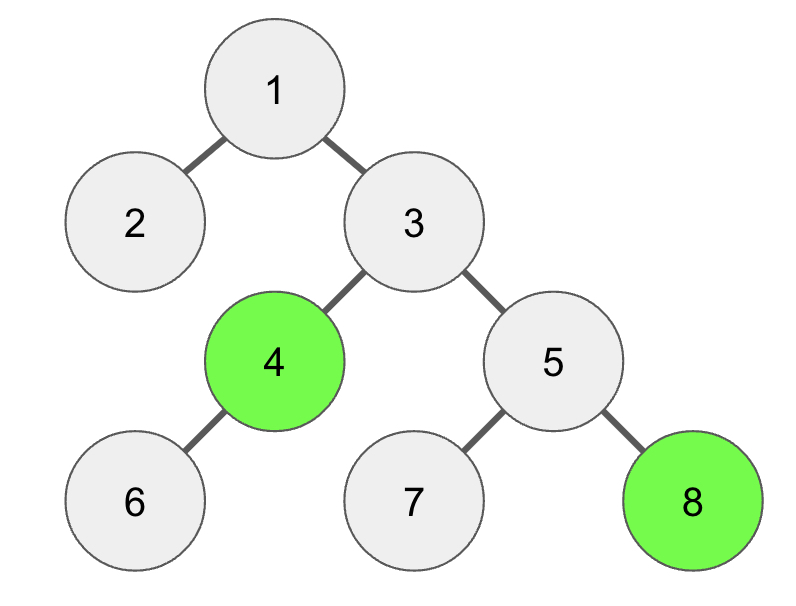
먼저 8번 노드의 깊이가 4번 노드보다 더 깊기 때문에 8에서 부모를 타고 올라가 깊이를 올려준다.
[깊이 맞추기]
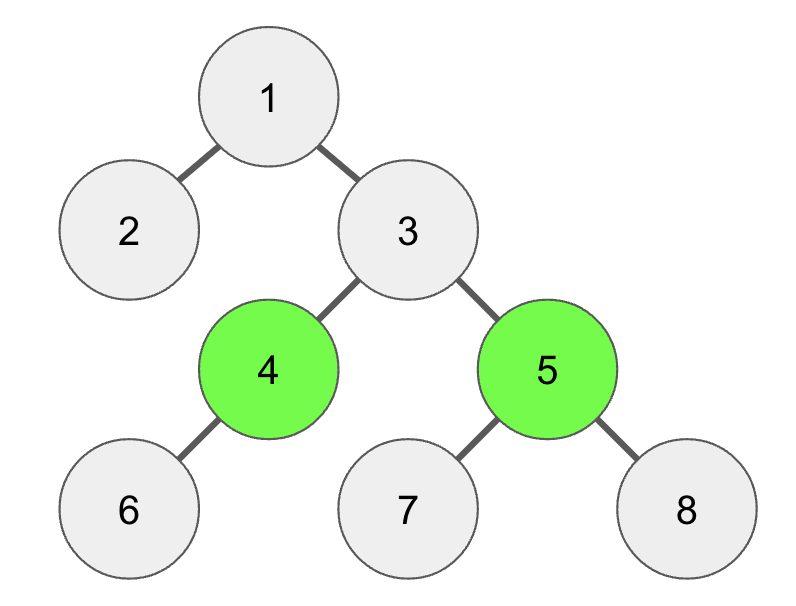
이제 두 노드가 같아질 때 까지 부모를 타고 노드의 깊이를 한 단계씩 높여주면 된다.
[공통 조상 찾기]
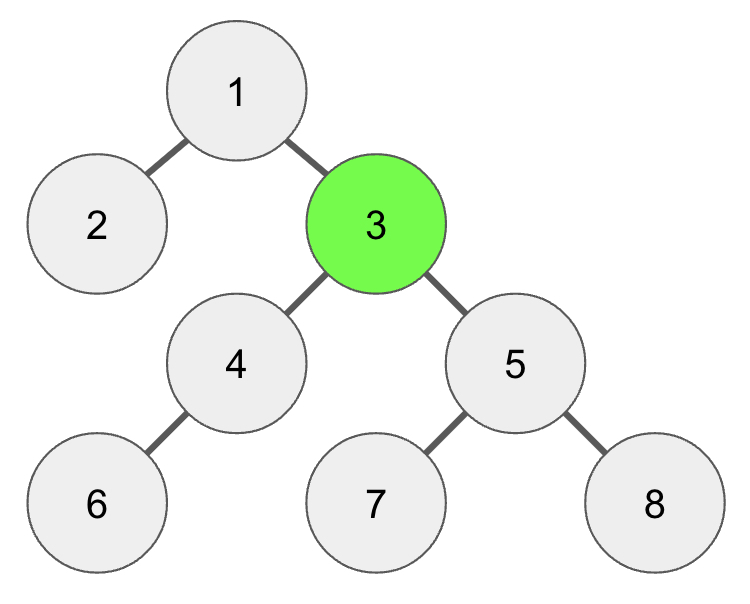
이런 식으로 4번 노드와 8번 노드의 공통 조상은 3번 노드인 것을 알 수 있다.
LCA 알고리즘에서는 깊이와 부모 노드의 정보가 필요하기 때문에 우선 BFS를 통해서 각 노드의 깊이와 부모를 찾아주어야 한다.
2.1.2 DP를 적용한 LCA
LCA의 시간복잡도는 최악의 경우 O(N)이다(제일 깊은 노드에서 공통조상이 루트일 경우)
이 문제는 N = 100,000이고 M = 100,000 이므로 시간복잡도가 10억을 넘어간다.
따라서 일반적인 LCA방식으로 문제를 풀게 되면 시간초과가 발생한다.
부모 노드를 따라 한 단계씩 노드를 탐색하기에는 시간이 너무 많이 소요된다.
만약 특정 노드와 연결된 모든 조상 노드들을 알고 있다면 한 단계씩 탐색하지 않아도 된다.
예를 들어, 다음과 같이 2번 노드와 8번 노드의 공통 조상을 찾는다고 하자
[공통 조상 찾기 예시_1]
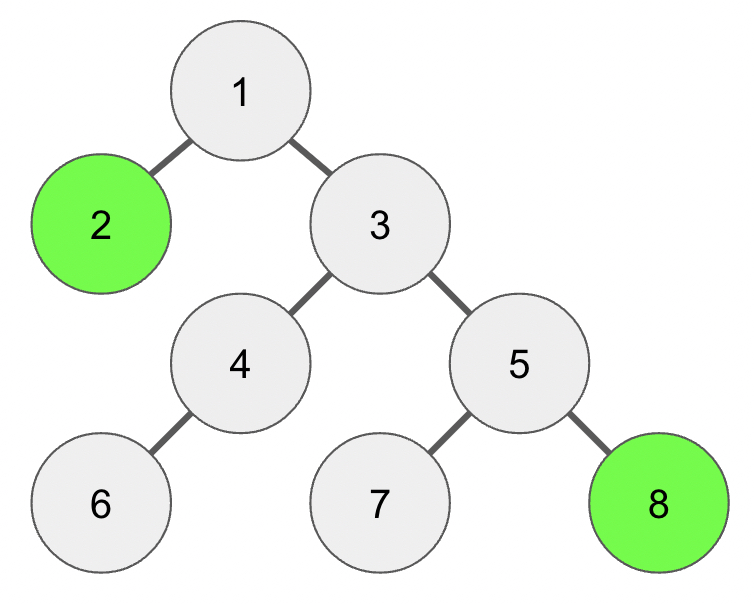
우선 8번 노드를 2번 노드와 깊이가 같아질 때까지 부모 노드를 따라 깊이를 줄여야 할 것이다.
그런데 만약 우리가 8번 노드와 연결된 조상 노드들을 모두 알고 있다면 어떨까?
8번 노드는 깊이가 3이므로 깊이를 2번 노드와 같은 1로 만들기 위해서는 8번 노드와 2번째로 연결된 조상을 찾으면 된다.
[공통 조상 찾기 예시_2]
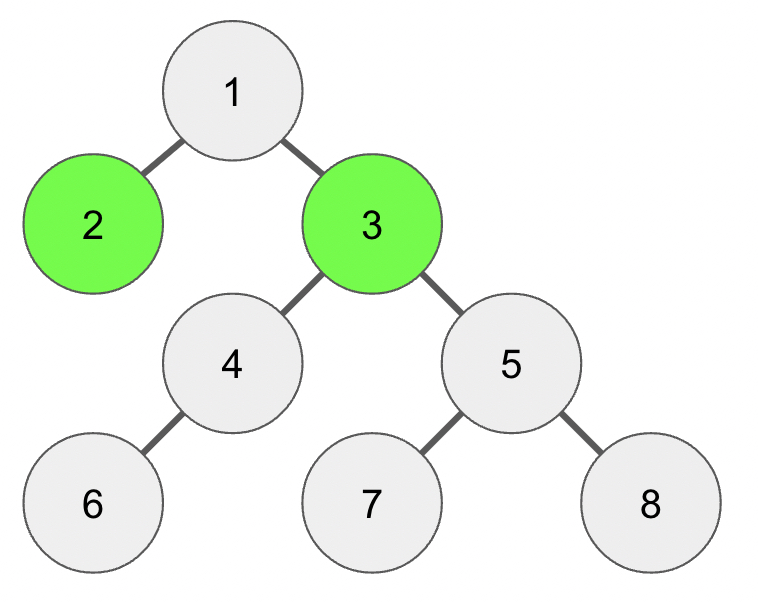
깊이를 맞추고 공통인 조상을 찾을 때도 연결된 조상 노드들을 알고 있다면 노드를 한 단계씩 탐색하는 것보다 더 빠르게 탐색할 수 있을 것이다.
그래서 특정 노드와 연결된 조상 노드들을 전부 구할 수 있을까?
답은 '아니다'이다
다만 특정 노드와 2^i 번째 연결된 조상 노드들은 점화식을 통해 그 값을 구할 수 있다.
Node.parent[i]를 Node와 2^i 번째 연결된 조상 노드라고 하자.
그러면 다음 점화식이 성립한다.
Node.parent[i] = Node.parent[i - 1].parent[i - 1]
Node와 2^i 번째 연결된 부모 노드는 Node와 2^(i-1) 번째 연결된 노드의 2^(i-1) 번째로 연결된 부모노드와 같다.
[점화식 예시_1]
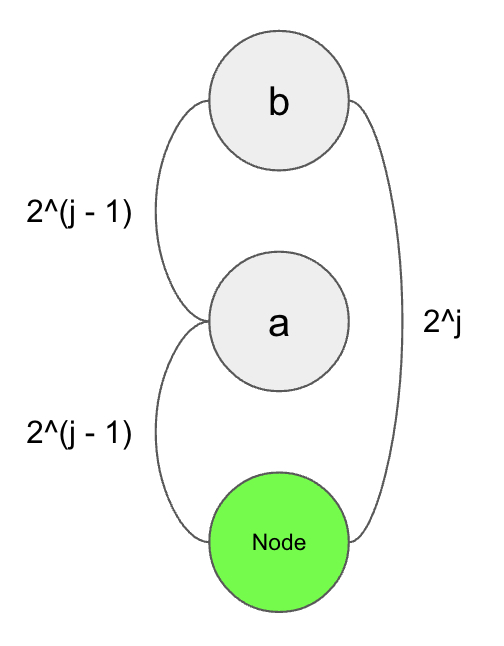
더 직관적으로 보기 위해서 예시를 하나 보자
다음과 같이 9번 노드에서 4(2^2)번 째로 연결된 조상 노드를 찾는다고 하자.
[점화식 예시_2]
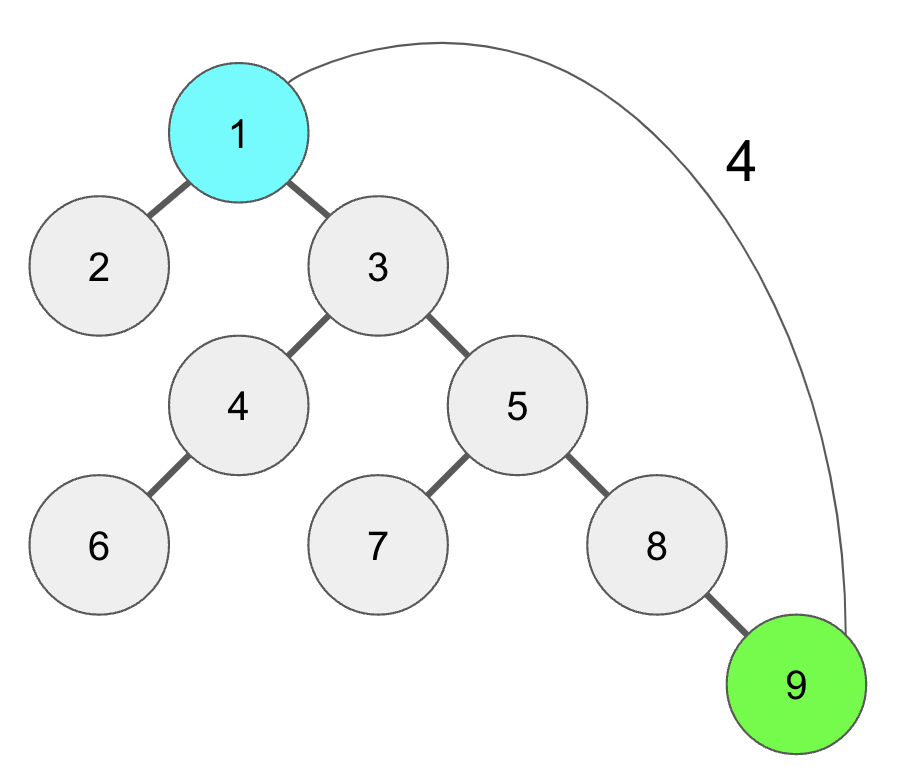
그러면 9번 노드에서 4(2^2)번째로 연결된 값은 9번 노드에서 2(2^1)번째로 연결된값인 5번 노드에서 2(2^1)번째 연결된 값이 된다.
[점화식 예시_3]
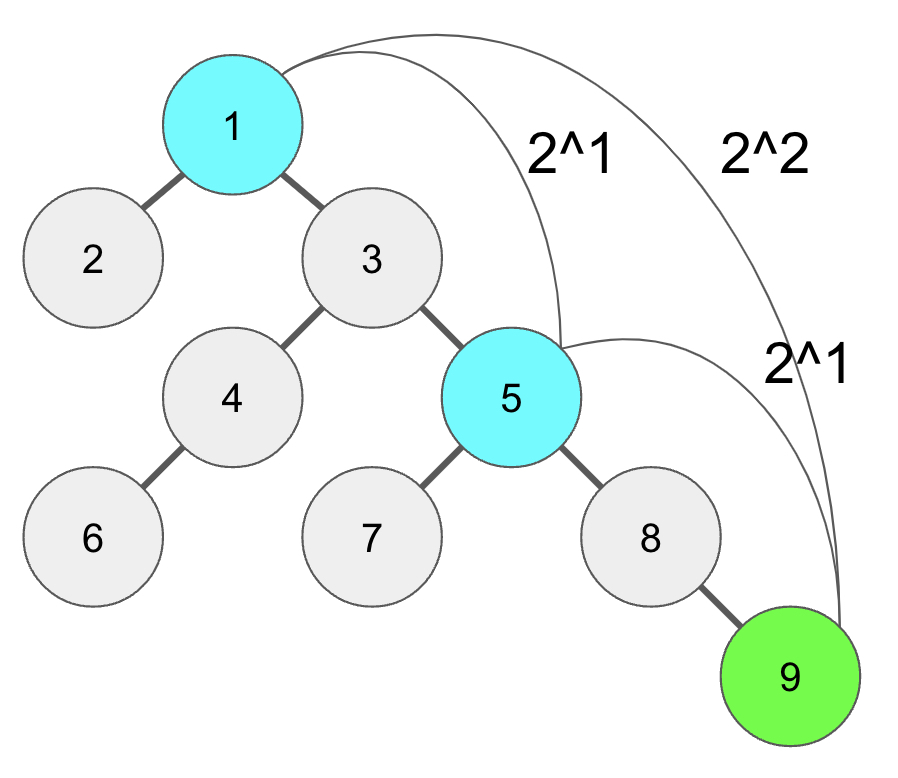
결론적으로 특정노드와 연결된 모든 조상을 구할 수는 없지만 2의 거듭제곱만큼 떨어진 조상 노드들은 구할 수 있다.
이진수를 사용하면 모든 수를 2의 거듭제곱으로 표현할 수 있으니 이진수를 사용해서 특정노드에서 n번째 연결된 조상 노드를 찾을 수 있다.
아래와 같은 트리에서 10번 노드와 5번째로 연결된 조상노드를 찾는다고 하자.
[2의 거듭제곱으로 조상 찾기_1]
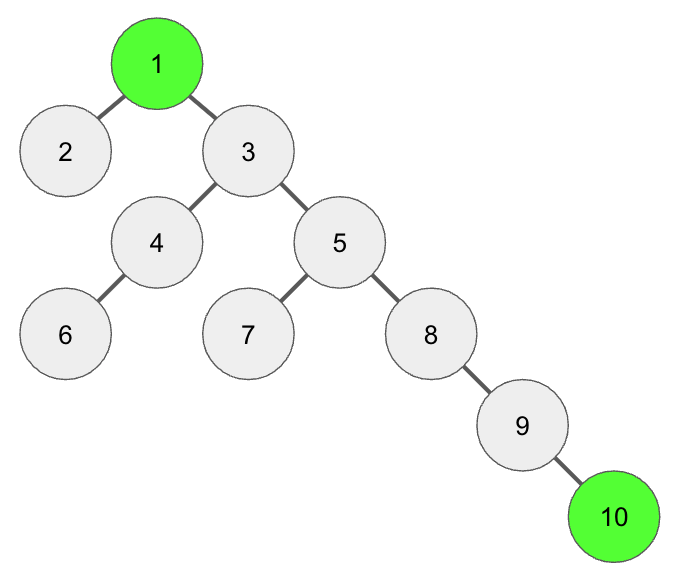
노드의 깊이를 depth라고 할 때, depth >= 2^k 를 만족하는 가장 큰 k를 구한다.
10번 노드의 깊이는 5이므로 위 식을 만족시키는 가장 큰 k는 2이다.
이제 2^2부터 2^0까지의 값을 depth에서 빼주면서 목표로 하는 노드(1번 노드)의 깊이보다 크거나 같을 경우 해당 노드로 이동한다.
위 예제의 경우 depth(5) - 2^2 = 1이므로 0(1번 노드의 깊이)보다 크다
따라서 깊이가 1인 노드로 이동한다.
깊이가 1인 노드는 10번 노드에서 2^2번째 연결된 조상이므로 3번 노드가 된다.
[2의 거듭제곱으로 조상 찾기_2]
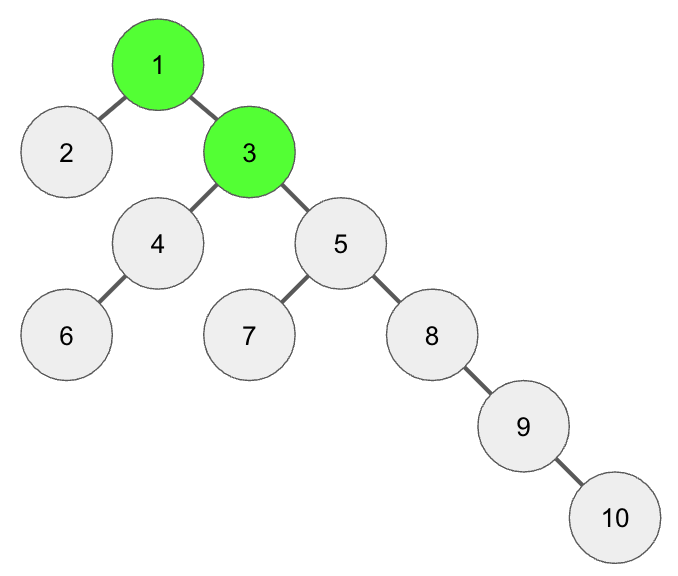
이제 현재 노드의 depth에서 2^1을 빼주자
depth(1) - 2 = -1으로 0(1번 노드의 깊이)보다 작다.
따라서 노드를 이동시키지 않는다.
마지막으로 depth에서 2^0을 빼주자
depth(1) - 2^0은 0으로 1번 노드의 깊이와 같다.
이제 노드를 2^0번째 연결된 조상으로 이동시키면 처음 10번 노드에서 5번째로 연결된 조상노드를 찾을 수 있다.
[2의 거듭제곱으로 조상 찾기_3]
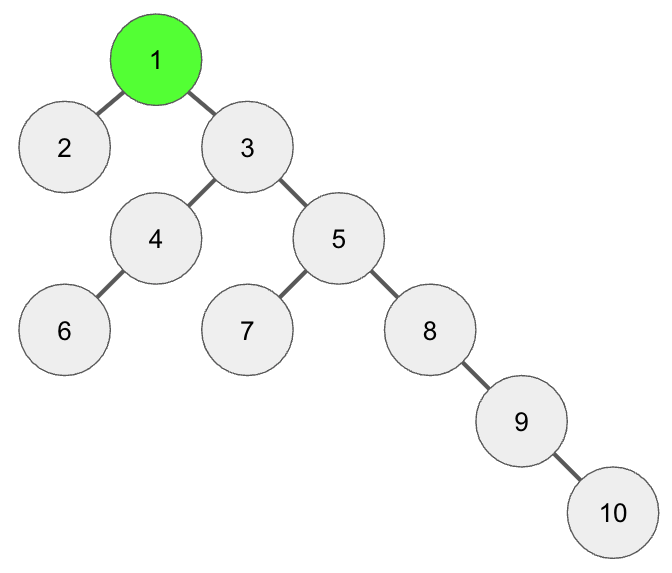
이처럼 이진수를 사용해서 4번째 조상노드, 1번째 조상노드를 통해 5번째 조상노드를 찾을 수 있다.
이 방법을 사용하면 n번 탐색하지 않고 log(n)번만 탐색할 수 있기 때문에 시간초과가 나지 않는다.
2.2 코드
2.2.1 Node
Node에 관련된 정보를 담고 있는 class이다.
[Node]
private static class Node {
int number;
boolean check = false;
int depth = 0;
//parent[i] => Node의 2^i번째 부모
Node[] parent;
List<Node> linkedNodeList = new ArrayList<>(); //[1]
public Node(int number, Node[] parent) {
this.number = number;
this.parent = parent;
}
}
LCA에서 사용될 깊이(depth)와 Node의 2^i 번째 부모를 담고있는 배열(parent)을 필드로 갖고 있다.
[1] : 연결된 노드 리스트
2.2.2 bfs
트리를 탐색하면서 LCA에 사용될 깊이(depth)와 부모에 대한 정보를 채워 넣는 메서드
[bfs]
private static void bfs(Node fistNode) {
Queue<Node> queue = new LinkedList<>();
fistNode.check = true;
queue.offer(fistNode);
while (!queue.isEmpty()) {
Node currentNode = queue.poll();
for (Node nextNode : currentNode.linkedNodeList) {
if (nextNode.check) {
continue;
}
nextNode.depth = currentNode.depth + 1;
nextNode.parent[0] = currentNode; //[1]
nextNode.check = true;
queue.offer(nextNode);
}
}
}
[1] : Node.parent[0]은 Node와 1(2^0)번째 연결된 조상을 뜻하므로 부모 노드를 의미한다.
2.2.3 dp
점화식을 통해 Node.parent를 구하는 메서드
[dp]
private static void dp(Node[] nodeArr) {
//j => parent의 인덱스.
//j가 2^j < node를 만족할때까지 탐색하며 값을 구한다.(가장 깊은 Node의 parent의 값을 구하기 위함)
for (int j = 1; (1<<j) < nodeArr.length; j++) { //[1]
for (int i = 1; i < nodeArr.length; i++) {
Node node = nodeArr[i];
//2^(j - 1)번째 부모가 없는 경우와 2^(j - 1)번째 부모의 j - 1번째 부모가 없을 경우는 넘어간다
if (node.parent[j - 1] == null || //[2]
nodeArr[node.parent[j - 1].number].parent[j - 1] == null) {
continue;
}
//점화식 => Node의 2^j번째 부모는 Node의 2^(j - 1)번째 부모의 2^(j - 1)번째 부모와 같다.
node.parent[j] = nodeArr[node.parent[j - 1].number].parent[j - 1];
}
}
}
j를 늘려가며 각 노드들과 2^j 번째 연결된 조상을 구한다.
[1] : 2^j < nodeArr.length를 만족할 때까지 j를 늘려가며 탐색을 하는 이유는 L개의 노드로 이루어진 트리에서 최대로 연결될 수 있는 거리는 L - 1 이기 때문이다.
[2] : 점화식을 구할 때 2^(j-1)번째 조상이 없는 경우와 2^(j-1)번째 조상에서 2^(j-1)번째 조상이 없는 경우, 즉 찾으려는 조상이 루트노드를 넘어간 경우는 continue로 넘어간다.
2.2.4 lca
dp로 구한 Node.parent배열을 적용한 LCA 알고리즘으로 두 노드 간 공통 조상을 찾는 메서드
[lca]
private static int lca(Node deepNode, Node shallowNode) {
if (deepNode.depth < shallowNode.depth) {
Node temp = deepNode;
deepNode = shallowNode;
shallowNode = temp;
}
//log => 깊은 Node의 깊이를 표현할 수 있는 2의 승수
//예) deepNode.depth가 13이면 log는 8이 되어야함(8 + 4 + 1 로 표현 가능)
int log = 1;
while ((1<<log) <= deepNode.depth) {
log++;
}
log--;
for (int i = log; i >= 0; i--) {
//deepNode의 깊이가 shallowNode와 같아질 때까지 깊이를 올려준다(parent배열을 사용)
if (deepNode.depth - (1<<i) >= shallowNode.depth) {
deepNode = deepNode.parent[i];
}
}
//deepNode와 shallowNode가 같을 경우 바로 return(불필요한 탐색을 없앰)
if (deepNode.number == shallowNode.number) {
return deepNode.number;
} else {
for (int i = log; i >= 0; i--) {
if (deepNode.parent[i] != null &&
deepNode.parent[i].number != shallowNode.parent[i].number) {
deepNode = deepNode.parent[i];
shallowNode = shallowNode.parent[i];
}
}
}
return deepNode.parent[0].number;
}
전체적인 틀은 기본적인 LCA와 같지만 공통 조상을 찾기 위해 깊이를 올리는 과정에서 dp를 사용한다.
2.3.4 main
[main]
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int nodeSize = Integer.parseInt(st.nextToken());
Node[] nodeArr = new Node[nodeSize + 1];
int log = 1;
while ((1 << log) <= nodeSize) {
log++;
}
for (int i = 0; i < nodeArr.length; i++) {
nodeArr[i] = new Node(i, new Node[log]);
}
for (int i = 1; i < nodeArr.length - 1; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
nodeArr[from].linkedNodeList.add(nodeArr[to]);
nodeArr[to].linkedNodeList.add(nodeArr[from]);
}
st = new StringTokenizer(br.readLine());
int caseSize = Integer.parseInt(st.nextToken());
bfs(nodeArr[1]);
dp(nodeArr);
while (caseSize-- > 0) {
st = new StringTokenizer(br.readLine(), " ");
int deepNumber = Integer.parseInt(st.nextToken());
int shallowNumber = Integer.parseInt(st.nextToken());
int ancestor = lca(nodeArr[deepNumber], nodeArr[shallowNumber]);
System.out.println(ancestor);
}
}
3. 전체 코드
[전체 코드]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class LCA2_11438 {
private static class Node {
int number;
boolean check = false;
int depth = 0;
//parent[i] => Node의 2^i번째 부모
Node[] parent;
List<Node> linkedNodeList = new ArrayList<>();
public Node(int number, Node[] parent) {
this.number = number;
this.parent = parent;
}
}
private static void bfs(Node fistNode) {
Queue<Node> queue = new LinkedList<>();
fistNode.check = true;
queue.offer(fistNode);
while (!queue.isEmpty()) {
Node currentNode = queue.poll();
for (Node nextNode : currentNode.linkedNodeList) {
if (nextNode.check) {
continue;
}
nextNode.depth = currentNode.depth + 1;
nextNode.parent[0] = currentNode;
nextNode.check = true;
queue.offer(nextNode);
}
}
}
private static void dp(Node[] nodeArr) {
//j => parent의 인덱스.
//j가 2^j < node를 만족할때까지 탐색하며 값을 구한다.(가장 깊은 Node의 parent의 값을 구하기 위함)
for (int j = 1; (1<<j) < nodeArr.length; j++) {
for (int i = 1; i < nodeArr.length; i++) {
Node node = nodeArr[i];
//2^(j - 1)번째 부모가 없는 경우와 2^(j - 1)번째 부모의 j - 1번째 부모가 없을 경우는 넘어간다
if (node.parent[j - 1] == null ||
nodeArr[node.parent[j - 1].number].parent[j - 1] == null) {
continue;
}
//점화식 => Node의 2^j번째 부모는 Node의 2^(j - 1)번째 부모의 2^(j - 1)번째 부모와 같다.
node.parent[j] = nodeArr[node.parent[j - 1].number].parent[j - 1];
}
}
}
private static int lca(Node deepNode, Node shallowNode) {
if (deepNode.depth < shallowNode.depth) {
Node temp = deepNode;
deepNode = shallowNode;
shallowNode = temp;
}
//log => 깊은 Node의 깊이를 표현할 수 있는 2의 승수
//예) deepNode.depth가 13이면 log는 8이 되어야함(8 + 4 + 1 로 표현 가능)
int log = 1;
while ((1<<log) <= deepNode.depth) {
log++;
}
log--;
for (int i = log; i >= 0; i--) {
//deepNode의 깊이가 shallowNode와 같아질 때까지 깊이를 올려준다(parent배열을 사용)
if (deepNode.depth - (1<<i) >= shallowNode.depth) {
deepNode = deepNode.parent[i];
}
}
//deepNode와 shallowNode가 같을 경우 바로 return(불필요한 탐색을 없앰)
if (deepNode.number == shallowNode.number) {
return deepNode.number;
} else {
for (int i = log; i >= 0; i--) {
if (deepNode.parent[i] != null &&
deepNode.parent[i].number != shallowNode.parent[i].number) {
deepNode = deepNode.parent[i];
shallowNode = shallowNode.parent[i];
}
}
}
return deepNode.parent[0].number;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int nodeSize = Integer.parseInt(st.nextToken());
Node[] nodeArr = new Node[nodeSize + 1];
int log = 1;
while ((1 << log) <= nodeSize) {
log++;
}
for (int i = 0; i < nodeArr.length; i++) {
nodeArr[i] = new Node(i, new Node[log]);
}
for (int i = 1; i < nodeArr.length - 1; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
nodeArr[from].linkedNodeList.add(nodeArr[to]);
nodeArr[to].linkedNodeList.add(nodeArr[from]);
}
st = new StringTokenizer(br.readLine());
int caseSize = Integer.parseInt(st.nextToken());
bfs(nodeArr[1]);
dp(nodeArr);
while (caseSize-- > 0) {
st = new StringTokenizer(br.readLine(), " ");
int deepNumber = Integer.parseInt(st.nextToken());
int shallowNumber = Integer.parseInt(st.nextToken());
int ancestor = lca(nodeArr[deepNumber], nodeArr[shallowNumber]);
System.out.println(ancestor);
}
}
}'알고리즘 > Graph' 카테고리의 다른 글
| 키 순-서 & 플로이드-워셜 알고리즘 (0) | 2024.08.02 |
|---|---|
| Union-Find 알고리즘을 케이크처럼 쉽게 이해하는법 (0) | 2023.02.07 |
| 줄-세우기 (0) | 2022.08.23 |



댓글