Union-Find
Union-Find 알고리즘은 다수의 노드로 트리를 만들 때 사용된다.
각 노드들을 병합해서 트리로 만드는 것이 Union
노드가 병합될 수 있는지를 확인하는것이 Find라서 Union-Find이다.
1. 노드로 트리 만들기
1부터 5까지의 노드가 있다고 하고 이 노드들로 트리를 만든다고 해보자
[노드]

우선 1과 2를 병합(연결) 할 수 있다
[1, 2 병합]

다음으로는 3과 4, 5를 병합해본다
[3과 4, 5 병합]

여기에 1과 3을 병합할 수 도 있다.
[1-3 병합]
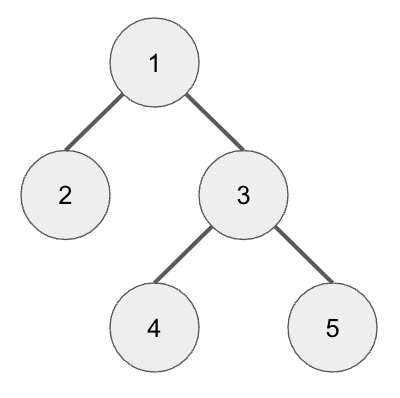
각각 연결된 노드가 있는 1과 3을 병합해도 트리가 되는 데는 문제가 없다.
그러나 2와 4는 병합할 수 없다
[병합 불가 경우]

왜냐하면 노드 2와 4는 같은 트리 내에 있는 노드이기 때문이다.
따라서 이 두 노드를 연결하게 되면 사이클이 발생한다.
트리는 사이클이 없는 그래프 구조이기 때문에 2와 4가 연결된 그래프는 트리가 아니게 된다.
따라서 2와 4는 병합할 수 없다.
2. Union-Find 개념
앞서 노드로 트리를 만들 때 우리는 각 노드들을 병합하는 것으로 트리를 만들었다.
동시에 노드를 병합했을 때 사이클이 발생하지 않도록 병합될 노드들이 같은 그룹에 있는지를 판단해야 했다.
이 같은 그룹인지 아닌지를 판단하게 해주는 것이 Find 알고리즘이다.
먼저 같은 그룹의 정의를 살펴보자
앞선 예시를 다시 봐보자
[두 그룹]

1, 2는 같은 그룹에 있고, 3, 4, 5는 같은 그룹에 있다는 것을 알 수 있다.
트리는 각 노드가 간선으로 연결되어 있기 때문에 반드시 특정 노드에서 다른 노드로 이동할 수 있다.
따라서 트리마다 루트노드를 정할 수 있다.
이 루트노드로 그룹을 판단한다.
루트노드가 같다면 같은 그룹 다르다면 다른 그룹이다.
예를 들어 다음과 같이 각 그룹에서 1과 3을 루트노드로 정할 수 있다.
[루트노드 설정]

이 상태에서는 2와 4의 노드를 병합할 수 있다.
왜냐하면 2의 루트노드는 1이고 4의 루트노드는 3이기 때문이다.
이는 2와 4가 다른 그룹에 있다는 것이고, 2와 4를 병합해도 사이클이 발생하지 않는다는 뜻이다.
[병합]

여기까지가 Find로 두 노드가 병합가능한지를 확인하는 과정이었다.
2와 4를 병합하니 루트노드가 두 개가 되는 문제가 있다.
트리는 하나의 루트노드를 갖는다.
때문에 1과 3 둘 중에 하나를 루트노드로 재설정해주면 된다.
여기서는 1을 선택했다.
[루트노드 병합]

두 노드를 병합해서 루트노드를 재설정하고 하나의 그룹으로 만드는 것이 Union이다
3. Union-Find
이제 진짜 Union-Find 알고리즘을 사용해서 트리를 만드는 과정을 확인해 보자
우선 각 노드들의 그룹을 표기해 줄 배열을 만든다.
[그룹 배열]

초기에 각 노드들은 자기 자신을 루트노드로 가질 수밖에 없다.
따라서 배열의 각 원소에는 자기 자신의 값을 갖는다.
[초기 세팅]

앞서 예제와 같이 1과 2를 병합한다.
1과 2는 각각 루트노드가 1과 2로 다른 그룹에 있기 때문에 병합할 수 있다.
[1-2 병합]

이제 1과 2는 하나의 그룹이 되었으니 루트노드를 하나로 정해줘야 한다
여기서는 1을 루트노드로 설정한다.
노드[2] = 노드[1]
[루트 노드 병합]

마찬가지로 3과 4,5도 병합할 수 있다.
루트노드는 3으로 한다.
[3,4,5 병합]

이제 2와 4를 병합해 보자
병합하기에 앞서 2의 루트노드와 4의 루트노드를 찾아야 한다.
배열의 원소값이 반드시 루트노드는 아니다.
때문에 원소값을 재귀적으로 탐색해서 루트노드를 찾아야 한다.
예를 들어 지금까지 완성된 배열로 2의 루트노드를 찾는다고 하자
[노드 2]

노드[2] = 1인데 1이 반드시 루트노드라는 뜻은 아니다
단지 2와 연결된 노드가 1이라는 것이다.
그렇다면 어떻게 루트노드를 찾을 수 있을까?
답은 간단하다
원소의 값이 연결된 노드를 뜻하는 것이라면 원소값 = Index가 될 때까지 값을 탐색하면 된다.
2와 연결된 노드는 1이라는 것을 알았으니 1번 노드로 가보자
[노드 1]

1번 노드의 원소값은 1이다
즉, 1번 노드는 루트노드이다.
따라서 2번 노드의 루트노드는 1이 된다.
이와 같이 그룹을 표기하는 배열의 원소값을 통해 재귀적으로 루트노드를 찾을 수 있다.
같은 원리로 4의 루트노드는 3이다.
따라서 두 노드의 루트노드가 다르기 때문에 충분히 병합 가능하다.
[2-4 병합]

루트노드는 1로 한다.
[루트노드 병합]

이번에는 1과 4를 연결해 보자
1은 배열에서 원소값 = Index이기 때문에 자기 자신 즉, 1이 루트노드이다.
4의 루트노드를 구해보자
앞서 말했지만 배열을 만든 방법상 배열의 원소값이 항상 루트노드는 아니다
따라서 원소값을 재귀적으로 탐색한다.
우선 4와 연결된 노드는 3이기 때문에 3을 확인한다.
[노드 3 확인]
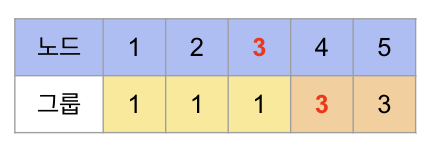
원소값 != Index이기 때문에 3은 루트노드가 아니다.
다시 3과 연결된 1로 가보자
[노드 1 확인]

1은 원소값=Index이므로 루트노드이다.
즉 4의 루트노드는 1이다
1과 4의 루트노드는 모두 1이다.
따라서 1과 4는 같은 그룹에 속해있고 병합할 경우 사이클이 발생하기 때문에 병합할 수 없다.
[병합 불가]

이런 식으로 Union-Find 알고리즘을 사용해서 트리를 만들 수 있다.
4. 코드
4.1 Find
[find]
private static int find(int[] groupArr, int index) {
if (groupArr[index] == index) {
return index;
}
return (groupArr[index] = find(groupArr, groupArr[index])); //[1]
}
앞선 예시와 같이 특정 number의 루트노드를 찾는 과정은 원소값 = index(groupArr[index] == index)가 되는 노드를 재귀적으로 탐색하는 것이다.
[1] : 앞서 방식으로 루트노드를 찾는 경우, 연결된 노드들을 탐색하면서 루트노드를 찾았다.
하지만 같은 노드를 탐색하는데 매번 연결된 노드를 탐색하는 것은 조금 비효율적이다(루트노드는 정해져 있기 때문)
따라서 특정 노드의 루트노드를 탐색할 때 연결된 노드들의 원소값을 전부 루트노드로 변경해 준다.
이 방식을 사용하면 한번 탐색된 노드의 루트노드를 탐색할 때는 한 번의 탐색으로 끝나게 된다.
예를 들어 아까의 예시와 같은 상황에서 4의 루트노드를 탐색할 때, 위 방식이 적용되면 배열은 다음과 같이 변화한다
[4의 루트노드 확인]

[4의 루트노드 탐색 과정]

재귀적으로 값이 탐색되고 Index = 1이 반환된다.
이제 재귀문을 순차적으로 빠져나오며 연결된 노드의 값이 루트노드로 변경된다.
[연결된 노드값을 루트노드로 변경]

이제 다음에 4의 루트노드를 탐색할 때는 한 번만 탐색하면 된다.
4.2 union
[union]
private static void union(int[] groupArr, int from, int to){
int fromRoot = find(from);
int toRoot = find(to);
if (fromRoot != toRoot) {
groupArr[toRoot] = groupArr[fromRoot];
}
}
각 루트노드를 탐색하고 루트노드가 다르다면 한쪽 루트노드 값을 다른 한쪽으로 변경한다.
'알고리즘 > Graph' 카테고리의 다른 글
| 키 순-서 & 플로이드-워셜 알고리즘 (0) | 2024.08.02 |
|---|---|
| LCA2 (0) | 2023.02.20 |
| 줄-세우기 (0) | 2022.08.23 |



댓글