키 순-서
백준 2456번 문제
https://www.acmicpc.net/problem/2458
1. 문제



2. 문제 풀이
2.1 아이디어
자신의 키 순서를 알기 위한 조건은 그래프상 모든 학생들과 연결되어 있어야 한다는 것이다.
예를 들어 5번은 3번과 6번에 연결되어 있지 않다.
이 때문에 3번과 6번이 자신과 비교해서 어디에 위치해 있는지 알 수 없기 때문에 순서를 매길 수 없다.
[순서를 알 수 없는 경우]

따라서 어떤 학생이 정방향과 역방향을 포함해서 모든 학생들과 연결되어 있으면 그 학생의 키 순서를 알 수 있다.
노드가 연결되어 있다는 것은 노드 간에 경로가 존재한다는 것이다.
때문에 모든 노드간 가능한 모든 경로를 탐색하는 플로이드-워셜 알고리즘을 사용해서 이 문제를 해결할 수 있다.
2.2 플로이드-워셜 알고리즘
플로이드-워셜 알고리즘은 그래프에서 모든 노드 간의 최단 경로(최소비용)를 찾는 알고리즘이다.
이 알고리즘은 연결 관점에서 그래프의 모든 노드 간의 가능한 모든 경로를 탐색하여 최단 경로(최소비용)를 계산한다.
플로이드-워셜 알고리즘은 다음과 같은 단계로 실행된다.
1. 초기화
- 그래프의 가중치 행렬 dist를 초기화 한다.
- dist[i][j]는 노드 i에서 노드 j로 가는 경로의 가중치를 나타낸다.
- 초기 상태의 dist 행렬은 노드 i에서 j로 직접 가는 경로의 가중치로 채워진다.
2. 중간 노드 고려
- 모든 노드 k를 중간 노드로 사용하여 경로를 갱신한다.
- 노드 k를 중간 노드로 사용하여, 모든 쌍의 노드 (i, j)에 대해 i -> k -> j 경로가 기존 i -> j 경로보다 짧은지 확인한다 .
[k = 5인 경우]

위 그래프에서 초기 dist[1][2] = ∞(직접 연결된 경로가 없기 때문) 이다.
이 때 k = 5일 경우 dist[1][5] + dist[5][1] 를 확인하고(경로 탐색) 그 값이 dist[1][2] 보다 작다면 갱신해준다.
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
3. 반복
- 위 과정을 모든 노드 k에 대해 반복한다.
- 모든 가능한 중간노드를 고려함으로써 연결된 모든 노드로 가는 경로를 탐색할 수 있고, 최소 비용을 구할 수 있다.
위 과정에서 점화식으로 값을 갱신하는 방식으로 볼때, 플로이드-워셜 알고리즘은 DP 알고리즘으로도 볼 수 있다.
그런데 플로이드-워셜 알고리즘은 k(중간 노드)를 1부터 순차적으로 증가하면서 경로를 탐색하는데 이러면 k의 순서에 따라 탐색하지 못하는 경로가 존재할 수 있지 않을까라는 의문이 들 수 도 있다.
이는 플로이드-워셜 알고리즘을 통해 그래프가 어떻게 탐색되는지 확인해보면 판단할 수 있다.
다음과 같은 그래프가 있다고 하자.
왠지 6에 직접 연결된게 5번이라 k = 5번 노드를 경유하는 경로를 탐색하면 k = 4번 노드를 경유하는 경로는 탐색하지 못할 것 같다.
이 그래프에서 6 -> 1로가는 경로를 탐색할 수 있을지를 확인해보자.
[플로이드-워셜 예시 그_1]

k, 즉 중간 노드는 1부터 증가하며 정해지기 때문에 다음과 같이 4를 경유하는 경로가 먼저 탐색된다.
[플로이드-워셜 예시 그_2]
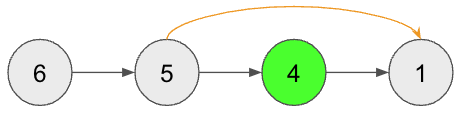
그 다음에는 k = 5로 탐색되는데 이 때 5 -> 1로 가는 경로가 이전 탐색에서 구해졌기 때문에,
6 -> 5 -> 1 의 순서로 탐색이 가능하다.
[플로이드-워셜 예시 그_3]
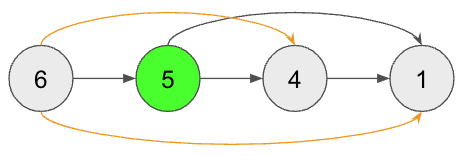
결과적으로 6 -> 1로 가는 경로를 탐색할 수 있다.
이처럼 플로이드-워셜 알고리즘은 중간 노드를 경유하는 경로를 탐색하며 모든 경로의 조각들을 구한다.
그리고 이 과정을 반복하면서 탐색된 경로의 조각들은 연결되게 되고 모든 경로를 탐색할 수 있다.
따라서 k(중간 노드)의 순서는 상관이 없고 노드가 연결만되어 있다면 가능한 모든 경로를 탐색할 수 있다.
2.3 플로이드-워셜 알고리즘을 통한 문제 풀이
플로이드-워셜 알고리즘의 노드간 모든 경로를 탐색한다는 점을 이용해서 문제를 해결한다.
2.3.1 findPath
모든 경로를 탐색해서 노드간 연결 상태를 확인하는 메서드.
경로를 탐색하며 최소비용을 계산할 필요는 없고 그저 노드가 연결 되어있는지를 판단하기만 하면된다.
따라서 가중치 행렬이아닌 연결여부를 확인하는 boolean형태의 배열을 만들고 플로이드-워셜 알고리즘을 적용한다.
초기값은 전부 false로 설정하고 직접 연결된 경로만 true로 해준다.
[findPaths]
public static void findPaths(boolean[][] path) {
for (int k = 0; k < path.length; k++) {
for (int i = 0; i < path.length; i++) {
for (int j = 0; j < path.length; j++) {
if (path[i][k] && path[k][j]) {
path[i][j] = true;
}
}
}
}
}
i와 j에 대해 k(중간노드)를 경유해서 연결되어 있다면 i -> j 경로가 있다는 뜻이므로 true값을 넣어준다.
위 방식을 사용하면 모든 경로를 탐색할 수 있고 모든 노드간 연결 여부를 확인 할 수 있다.
2.3.2 getResult
키 순서를 알 수 있는 학생(노드)을 카운트하고 반환하는 메서드
연결상태 행렬으로 노드가 특정 노드와 정방향과 역방향을 포함해서 연결되어있는지를 확인하고 카운트한다.
카운트한 값이 전체 노드갯수 - 1(자신 제외)와 동일하다면 순위를 알 수 있는 학생이기 때문에 결과값을 증가시켜준다.
[getResult]
private static int getResult(int size, boolean[][] path) {
int result = 0;
for (int i = 0; i < size; i++) {
int count = 0;
for (int j = 0; j < size; j++) {
if (path[i][j] || path[j][i]) {
count++;
}
}
if (count == size - 1) {
result++;
}
}
return result;
}
3. 전체 코드
[전체 코드]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class 키_순서_2458 {
public static void findPaths(boolean[][] path) {
for (int k = 0; k < path.length; k++) {
for (int i = 0; i < path.length; i++) {
for (int j = 0; j < path.length; j++) {
if (path[i][k] && path[k][j]) {
path[i][j] = true;
}
}
}
}
}
private static int getResult(int size, boolean[][] path) {
int result = 0;
for (int i = 0; i < size; i++) {
int count = 0;
for (int j = 0; j < size; j++) {
if (path[i][j] || path[j][i]) {
count++;
}
}
if (count == size - 1) {
result++;
}
}
return result;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] inputSize = br.readLine().split(" ");
int size = Integer.parseInt(inputSize[0]);
int edgeSize = Integer.parseInt(inputSize[1]);
boolean[][] path = new boolean[size][size];
for (int i = 0; i < edgeSize; i++) {
String[] inputEdge = br.readLine().split(" ");
int from = Integer.parseInt(inputEdge[0]);
int to = Integer.parseInt(inputEdge[1]);
path[from - 1][to - 1] = true;
}
findPaths(path);
System.out.println(getResult(size, path));
}
}
'알고리즘 > Graph' 카테고리의 다른 글
| LCA2 (0) | 2023.02.20 |
|---|---|
| Union-Find 알고리즘을 케이크처럼 쉽게 이해하는법 (0) | 2023.02.07 |
| 줄-세우기 (0) | 2022.08.23 |



댓글